初中数学菱形的性质试题

如图，在平面直角坐标系中，有抛物线．抛物线经过原点，与轴正半轴交于点，与其对称轴交于点，是抛物线上一点，且在轴上方，过点作轴的垂线交抛物线于点，过点作的垂线交抛物线于点（不与点重合），连结，设点的横坐标为．

（1）求的值；

（2）当抛物线经过原点时，设与重叠部分图形的周长为．

①求的值；

②求与之间的函数关系式；

（3）当为何值时，存在点，使以点，，，为顶点的四边形是轴对称图形？直接写出的值．

如图，在菱形中，对角线与相交于点，，，点从点出发，沿以每秒2个单位长度的速度向终点运动，当点不与点重合时，过点作于点，作交于点，过点作交（或的延长线）于点，得到矩形，设点运动的时间为秒

（1）求线段的长（用含的代数式表示）；

（2）求点与点重合时的值；

（3）设矩形与菱形重叠部分图形的面积与平方单位，求与之间的函数关系式；

（4）矩形的对角线与相交于点，当时，的值为　　；当时，的值为　　．

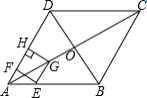
如图，在平面直角坐标系中，菱形的顶点在轴正半轴上，顶点的坐标为，是抛物线上一点，且在轴上方，则面积的最大值为　　．

如图，菱形 $\mathit{ABCD}$ 中， $\angle D=150°$ ，则 $\angle 1=($ 　　 $)$

A．

$30°$

B．

$25°$

C．

$20°$

D．

$15°$

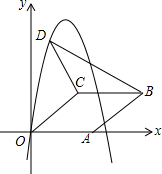
求证：菱形的两条对角线互相垂直．

已知：如图，四边形 $\mathit{ABCD}$ 是菱形，对角线 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $O$ ．

求证： $\mathit{AC}\perp \mathit{BD}$ ．

以下是排乱的证明过程：

①又 $\mathit{BO}=\mathit{DO}$ ；

② $\therefore \mathit{AO}\perp \mathit{BD}$ ，即 $\mathit{AC}\perp \mathit{BD}$ ；

③ $\because$ 四边形 $\mathit{ABCD}$ 是菱形；

④ $\therefore \mathit{AB}=\mathit{AD}$ ．

证明步骤正确的顺序是 $($ 　　 $)$

A．

③ $\to$ ② $\to$ ① $\to$ ④

B．

③ $\to$ ④ $\to$ ① $\to$ ②

C．

① $\to$ ② $\to$ ④ $\to$ ③

D．

① $\to$ ④ $\to$ ③ $\to$ ②

如图，在菱形中，为对角线，点，分别在，上，，连接．

（1）求证：；

（2）延长交的延长线于点，连接交于点．若，，求的长．

把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为　　．

如图，菱形的对角线，相交于点，是的中点，点，在上，，．

（1）求证：四边形是矩形；

（2）若，，求和的长．

（年贵州省黔南州）如图，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上．若∠BAD=120°，则弧BC的长度等于     （结果保留π）．

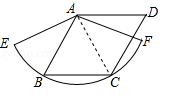
（年云南省曲靖市）如图，菱形ABCD的对角线AC与BD相交于点O，且BE∥AC，CE∥BD．

（1）求证：四边形OBEC是矩形；
（2）若菱形ABCD的周长是，tanα=，求四边形OBEC的面积．

（年新疆、生产建设兵团）如图，四边形ABCD为菱形，点E为对角线AC上的一个动点，连结DE并延长交AB于点F，连结BE．
（1）如图①，求证：∠AFD=∠EBC；
（2）如图②，若DE=EC且BE⊥AF，求∠DAB的度数；
（3）若∠DAB=90°且当△BEF为等腰三角形时，求∠EFB的度数（只写出条件与对应的结果）

（年贵州省铜仁市）已知一个菱形的两条对角线长分别为6cm和8cm，则这个菱形的面积为             cm²．

（年新疆乌鲁木齐市）若菱形的周长为8，相邻两内角之比为3：1，则菱形的高是     ．

（年贵州省黔东南州）如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（ ）

A．

B．

C．12

D．24

（年云南省昆明市）如图，在菱形ABCD中，对角线AC、BD相交于点O，下列结论：①AC⊥BD；②OA=OB；③∠ADB=∠CDB；④△ABC是等边三角形，其中一定成立的是（ ）

A．①②      B．③④      C．②③      D．①③