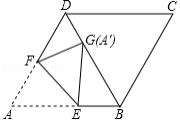
如图,在菱形 中, ,将菱形折叠,使点 恰好落在对角线 上的点 处(不与 、 重合),折痕为 ,若 , ,则 的长为 .
如图,菱形 的顶点 、 在 轴上 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于

A. B. C. D.3
如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长为

A.24B.18C.12D.9
如图,点 ,点 分别在菱形 的边 , 上,且 , 交 于点 ,延长 交 的延长线于 ,若 ,则 的值为

A. B. C. D.
如图,在菱形 中, , ,将菱形 绕点 逆时针方向旋转,对应得到菱形 ,点 在 上, 与 交于点 ,则 的长是 .

下列结论中,矩形具有而菱形不一定具有的性质是
A.内角和为 B.对角线互相平分
C.对角线相等D.对角线互相垂直
如图,在菱形 中,对角线 与 相交于点 ,若 , ,则 的长为

A.2B.3C. D.
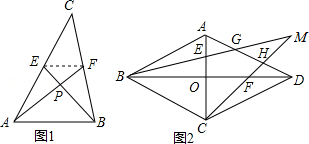
尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且 ,垂足为P,设 .
求证:
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故 ,设 ,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求 的值.
如图,菱形 的对角线 与 交于点 , , , 是 的中点,则 的周长是

A.18B.16C.9D.8
菱形 的周长为8, ,以 为腰,在菱形外作底角是 的等腰 ,连接 , .请画出图形,并直接写出 的面积.
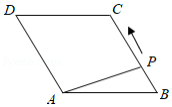
如图,菱形 中, ,点 从点 出发,沿折线 方向移动,移动到点 停止.在 形状的变化过程中,依次出现的特殊三角形是
| A. |
直角三角形 等边三角形 等腰三角形 直角三角形 |
| B. |
直角三角形 等腰三角形 直角三角形 等边三角形 |
| C. |
直角三角形 等边三角形 直角三角形 等腰三角形 |
| D. |
等腰三角形 等边三角形 直角三角形 等腰三角形 |
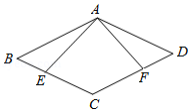
如图,四边形 是菱形,点 , 分别在 , 边上,添加以下条件不能判定 的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在菱形 中, , 是锐角, 于点 , 是 的中点,连接 , .若 ,则 的值为 .
