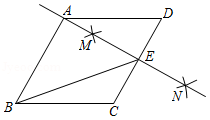
如图,在菱形 ABCD中,按以下步骤作图:
①分别以点 C和点 D为圆心,大于 CD为半径作弧,两弧交于点 M, N;
②作直线 MN,且 MN恰好经过点 A,与 CD交于点 E,连接 BE,
则下列说法错误的是( )
| A. |
∠ABC=60° |
B. |
S △ ABE=2S △ ADE |
| C. |
若AB=4,则BE= |
D. |
sin∠CBE= |
如图,菱形 的对角线 、 的长分别为6和8,则这个菱形的周长是

A.20B.24C.40D.48
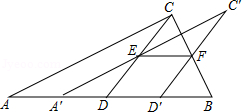
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,菱形 的对角线 与 交于点 , , , .
(1)求 的值;
(2)求证:四边形 是矩形.

如图,将边长为4的菱形 ABCD纸片折叠,使点 A恰好落在对角线的交点 O处,若折痕 EF=2 ,则∠ A=( )

| A. |
120° |
B. |
100° |
C. |
60° |
D. |
30° |
菱形具有而一般平行四边形不具有的性质是
A.对边相等B.对角相等
C.对角线互相平分D.对角线互相垂直
定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形 中, , ,过点 作 垂线交 的延长线于点 ,且 ,证明:四边形 是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形 内接于 中, .求 的半径.

如图,在平面直角坐标系中,点 为坐标原点,菱形 的顶点 的坐标为 .
(1)求过点 的反比例函数 的解析式;
(2)连接 ,过点 作 交 轴于点 ,求直线 的解析式.

如图,在菱形 中, , .动点 从点 出发,以每秒1个单位长度的速度沿折线 运动到点 ,同时动点 从点 出发,以相同速度沿折线 运动到点 ,当一个点停止运动时,另一点也随之停止.设 的面积为 ,运动时间为 秒.则下列图象能大致反映 与 之间函数关系的是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在周长为12的菱形 中,
中, ,
, ,若
,若 为对角线
为对角线 上一动点,则
上一动点,则 的最小值为
的最小值为


A.1B.2C.3D.4
如图,菱形 中, ,点 从点 出发,沿折线 方向移动,移动到点 停止.在 形状的变化过程中,依次出现的特殊三角形是
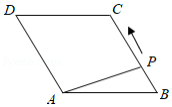
| A. |
直角三角形 等边三角形 等腰三角形 直角三角形 |
| B. |
直角三角形 等腰三角形 直角三角形 等边三角形 |
| C. |
直角三角形 等边三角形 直角三角形 等腰三角形 |
| D. |
等腰三角形 等边三角形 直角三角形 等腰三角形 |
如图,四边形 是菱形,点 , 分别在 , 边上,添加以下条件不能判定 的是
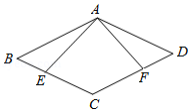
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在菱形 中, , 是锐角, 于点 , 是 的中点,连接 , .若 ,则 的值为 .
