如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知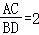 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

点 、 为半径是3的圆周上两点,点 为 的中点,以线段 、 为邻边作菱形 ,顶点 恰在该圆直径的三等分点上,则该菱形的边长为
A. 或 B. 或 C. 或 D. 或
如图,平面直角坐标系中,菱形 在第一象限内,边 与 轴平行, , 两点的纵坐标分别为6,4,反比例函数 的图象经过 , 两点,若菱形 的面积为 ,则 的值为 .

小敏思考解决如下问题:
原题:如图1,点 , 分别在菱形 的边 , 上, ,求证: .

(1)小敏进行探索,若将点 , 的位置特殊化;把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2.此时她证明了 ,请你证明.
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.
(3)如果在原题中添加条件: , ,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
一张菱形纸片 的边长为 ,高 等于边长的一半,将菱形纸片沿直线 折叠,使点 与点 重合,直线 交直线 于点 ,则 的长为 .
如图,在四边形 中, , , , ,动点 自 点出发,沿着边 向点 匀速运动,同时动点 自点 出发,沿着边 匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点 运动 (秒 时, 的面积为 ,则 关于 的函数图象是

A. B.
B.
C. D.
D.
如图,在边长为的菱形
中,
,点
,
分别是
,
上的动点,且
,
与
交于点
.当点
从点
运动到点
时,则点
的运动路径长为 .
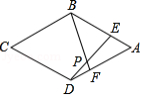
如图,点 在菱形 的 边上,点 在 边的延长线上,连接 , ,对于下列条件:① ;② , ;③ ;④ .只选取其中一条添加,不能确定 的是

| A. |
① |
B. |
② |
C. |
③ |
D. |
④ |
【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .


如图,在菱形 中, 是对角线 上一动点,过点 作 于点 . 于点 .若菱形 的周长为20,面积为24,则 的值为

| A. |
4 |
B. |
|
C. |
6 |
D. |
|
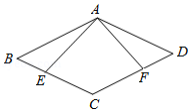
如图,四边形 是菱形,点 , 分别在 , 边上,添加以下条件不能判定 的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在菱形 中, , 是锐角, 于点 , 是 的中点,连接 , .若 ,则 的值为 .

如图,菱形 的边长为6, , 是 边的一个三等分点, 是对角线 上的动点,当 的值最小时, 的长是

A. B. C. D.