小敏思考解决如下问题:
原题:如图1,点 , 分别在菱形 的边 , 上, ,求证: .
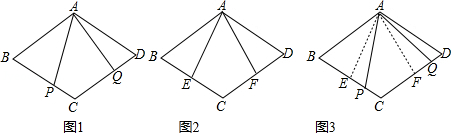
(1)小敏进行探索,若将点 , 的位置特殊化;把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2.此时她证明了 ,请你证明.
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.
(3)如果在原题中添加条件: , ,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
相关知识点
推荐套卷
 ,射线AG∥BC,点E从点A出发沿射线AG以
,射线AG∥BC,点E从点A出发沿射线AG以 的速度运动,同时点F从点B出发沿射线BC以
的速度运动,同时点F从点B出发沿射线BC以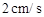 的速度运动,设运动时间为
的速度运动,设运动时间为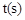
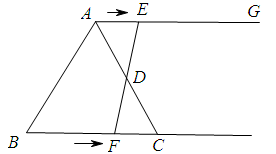
 为s时,四边形ACFE是菱形;
为s时,四边形ACFE是菱形;


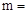 ,
,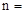 ,扇形统计图中E组所占的百分比为%。
,扇形统计图中E组所占的百分比为%。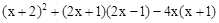 ,其中
,其中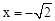
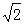 ,P是AC上的一个动点.
,P是AC上的一个动点.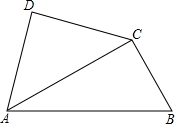
 粤公网安备 44130202000953号
粤公网安备 44130202000953号