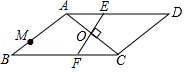
如图,在▱ ABCD中,∠ B=30°, AB= AC, O是两条对角线的交点,过点 O作 AC的垂线分别交边 AD, BC于点 E, F;点 M是边 AB的一个三等分点,则△ AOE与△ BMF的面积比为 .
如图,在 中,
中, ,
, ,
,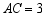 ,点
,点 、
、 分别是
分别是 、
、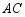 的中点,点
的中点,点 、
、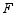 在
在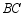 边上(均不与端点重合),
边上(均不与端点重合),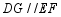 .将
.将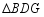 绕点
绕点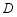 顺时针旋转
顺时针旋转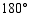 ,将
,将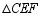 绕点
绕点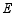 逆时针旋转
逆时针旋转 ,拼成四边形
,拼成四边形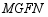 ,则四边形
,则四边形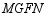 周长
周长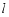 的取值范围是 .
的取值范围是 .
如图,四边形 ABCO是平行四边形, OA=2, AB=6,点 C在 x轴的负半轴上,将▱ ABCO绕点 A逆时针旋转得到▱ ADEF, AD经过点 O,点 F恰好落在 x轴的正半轴上,若点 D在反比例函数 y= ( x<0)的图象上,则 k的值为 .

如图,在▱ ABCD中, AB=3, BC=5,以点 B的圆心,以任意长为半径作弧,分别交 BA、 BC于点 P、 Q,再分别以 P、 Q为圆心,以大于 PQ的长为半径作弧,两弧在∠ ABC内交于点 M,连接 BM并延长交 AD于点 E,则 DE的长为 .

如图,在平行四边形 中,点 为边 上一点, ,点 ,点 分别是 , 中点,若 ,则 的长为 .

如图,平行四边形 的顶点 在反比例函数 的图象上,点 在 轴上,点 ,点 在 轴上, 与 轴交于点 ,若 ,则 的值为 .

如图,在平行四边形 中,点 是 的中点, , 的延长线交于点 .若 的面积为1,则四边形 的面积为 .

如图,在中,
,
,
,点
为边
上的一个动点,连接
并延长至点
,使得
,以
、
为邻边构造
,连接
,则
的最小值为 .

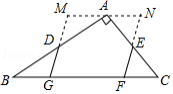
在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,是
的对角线,点
在
上,
,
,则
的大小是 .

以对角线的交点
为原点,平行于
边的直线为
轴,建立如图所示的平面直角坐标系.若
点坐标为
,则
点坐标为 .

规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若、
的坐标分别为
,
,
是二次函数
的图象上在第一象限内的任意一点,
垂直直线
于点
,则四边形
是广义菱形.其中正确的是 .(填序号)