初中数学平行四边形的性质填空题

四边形具有不稳定性．如图，矩形 $\mathit{ABCD}$按箭头方向变形成平行四边形 $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$，当变形后图形面积是原图形面积的一半时，则 $\angle A^{\text{'}}=$　　．

将平行四边形 $\mathit{OABC}$放置在如图所示的平面直角坐标系中，点 $O$为坐标原点．若点 $A$的坐标为 $(3,0)$，点 $C$的坐标为 $(1,2)$，则点 $B$的坐标为　　．

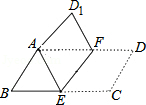
如图，面积为6的平行四边形纸片 $\mathit{ABCD}$中， $\mathit{AB}=3$， $\angle \mathit{BAD}=45°$，按下列步骤进行裁剪和拼图．

第一步：如图①，将平行四边形纸片沿对角线 $\mathit{BD}$剪开，得到 $\mathit{\Delta ABD}$和 $\mathit{\Delta BCD}$纸片，再将 $\mathit{\Delta ABD}$纸片沿 $\mathit{AE}$剪开 $(E$为 $\mathit{BD}$上任意一点），得到 $\mathit{\Delta ABE}$和 $\mathit{\Delta ADE}$纸片；

第二步：如图②，将 $\mathit{\Delta ABE}$纸片平移至 $\mathit{\Delta DCF}$处，将 $\mathit{\Delta ADE}$纸片平移至 $\mathit{\Delta BCG}$处；

第三步：如图③，将 $\mathit{\Delta DCF}$纸片翻转过来使其背面朝上置于 $\mathit{\Delta PQM}$处（边 $\mathit{PQ}$与 $\mathit{DC}$重合， $\mathit{\Delta PQM}$和 $\mathit{\Delta DCF}$在 $\mathit{DC}$同侧），将 $\mathit{\Delta BCG}$纸片翻转过来使其背面朝上置于 $\mathit{\Delta PRN}$处，（边 $\mathit{PR}$与 $\mathit{BC}$重合， $\mathit{\Delta PRN}$和 $\mathit{\Delta BCG}$在 $\mathit{BC}$同侧）．

则由纸片拼成的五边形 $\mathit{PMQRN}$中，对角线 $\mathit{MN}$长度的最小值为　　．

如图， $▱\mathit{ABCD}$中， $\mathit{AC}=8$， $\mathit{BD}=6$， $\mathit{AD}=a$，则 $a$的取值范围是　　．

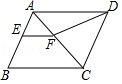
如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D₁，折痕为EF，若 $\angle \mathit{BAE}＝55°$，则 $\angle D_1\mathit{AD}＝$　　．

已知：在平行四边形ABCD中，点E在直线AD上， $\mathit{AE}=\frac{1}{3}\mathit{AD}$，连接CE交BD于点F，则 $\mathit{EF}：\mathit{FC}$的值是　　．

如图，若以平行四边形一边 AB为直径的圆恰好与对边 CD相切于点 D，则∠ C＝ 　　度．

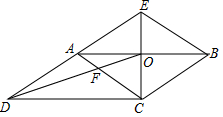
如图， CE是▱ ABCD的边 AB的垂直平分线，垂足为点 O， CE与 DA的延长线交于点 E．连接 AC， BE， DO， DO与 AC交于点 F，则下列结论：

①四边形 ACBE是菱形；

②∠ ACD＝∠ BAE；

③ AF： BE＝2：3；

④ S _{四边形 AFOE}： S _{△ COD}＝2：3．

其中正确的结论有 　　．（填写所有正确结论的序号）

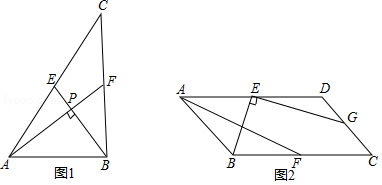
如图1， AF， BE是△ ABC的中线， AF⊥ BE，垂足为点 P，设 BC＝ a， AC＝ b， AB＝ c，则 a ²+ b ²＝5 c ²，利用这一性质计算．如图2，在▱ ABCD中， E， F， G分别是 AD， BC， CD的中点， EB⊥ EG于点 E， AD＝8， AB＝2 $\sqrt{5}$ ，则 AF＝ 　　．

如图， P是▱ ABCD的边 AD上一点， E、 F分别是 PB、 PC的中点，若▱ ABCD的面积为16 cm ²，则△ PEF的面积（阴影部分）是 　　 cm ²．

如图，在▱ ABCD中， AC是一条对角线， EF∥ BC，且 EF与 AB相交于点 E，与 AC相交于点 F，3 AE＝2 EB，连接 DF．若 S _{△ AEF}＝1，则 S _{△ ADF}的值为 　　．

如图，将平行四边形 ABCD沿对角线 BD折叠，使点 A落在点 A′处，∠1＝∠2＝48°，则∠ A′的度数为 　 　．

如图，在▱ABCD中， $\mathit{AB}=2\sqrt{13}\text{cm}$， $\mathit{AD}＝4\mathit{cm}，$ $\mathit{AC}\perp \mathit{BC}$，则△DBC比△ABC的周长长　　cm．

已知平行四边形 ABCD的顶点 A在第三象限，对角线 AC的中点在坐标原点，一边 AB与 x轴平行且 AB＝2，若点 A的坐标为（ a， b），则点 D的坐标为 　．

在▱ ABCD中， AE平分∠ BAD交边 BC于 E， DF平分∠ ADC交边 BC于 F，若 AD＝11， EF＝5，则 AB＝ 　　．