初中数学多边形试题

下列长度的三条线段与长度为5的线段能组成四边形的是 $($ 　　 $)$

A．

1，1，1

B．

1，1，8

C．

1，2，2

D．

2，2，2

各顶点都在方格纸的格点（横竖格子线的交错点）上的多边形称为格点多边形，它的面积 $S$可用公式 $S=a+\frac{1}{2}b-1(a$是多边形内的格点数， $b$是多边形边界上的格点数）计算，这个公式称为“皮克 $\left(\mathit{Pick}\right)$定理”．如图给出了一个格点五边形，则该五边形的面积 $S=$　　．

如图， $\odot O$与正五边形 $\mathit{ABCDE}$的边 $\mathit{AB}$、 $\mathit{DE}$分别相切于点 $B$、 $D$，则劣弧 $\widehat{\mathit{BD}}$所对的圆心角 $\angle \mathit{BOD}$的大小为　 　度．

若正多边形的每一个内角为 $135°$，则这个正多边形的边数是　　．

如图，正五边形 $\mathit{ABCDE}$的边长为2，连接 $\mathit{AC}$、 $\mathit{AD}$、 $\mathit{BE}$， $\mathit{BE}$分别与 $\mathit{AC}$和 $\mathit{AD}$相交于点 $F$、 $G$，连接 $\mathit{DF}$，给出下列结论：① $\angle \mathit{FDG}=18°$；② $\mathit{FG}=3-\sqrt{5}$；③ ${\left(S_{\mathit{四边形CDEF}}\right)}^2=9+2\sqrt{5}$；④ $D{F}^2-D{G}^2=7-2\sqrt{5}$．其中结论正确的个数是 $($　　 $)$

A．1B．2C．3D．4

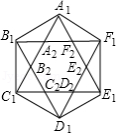
如图，正六边形 $A_1{B}_1{C}_1{D}_1{E}_1{F}_1$的边长为1，它的六条对角线又围成一个正六边形 $A_2{B}_2{C}_2{D}_2{E}_2{F}_2$，如此继续下去，则正六边形 $A_4{B}_4{C}_4{D}_4{E}_4{F}_4$的面积是　　．

如图，以正方形 $\mathit{ABCD}$的 $\mathit{AB}$边向外作正六边形 $\mathit{ABEFGH}$，连接 $\mathit{DH}$，则 $\angle \mathit{ADH}=$　　度．

如图，正五边形 $\mathit{ABCDE}$中，对角线 $\mathit{AC}$与 $\mathit{BE}$相交于点 $F$，则 $\angle \mathit{AFE}=$　　度．

我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于 $3)$，可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．

（1）已知凸五边形 $\mathit{ABCDE}$的各条边都相等．

①如图1，若 $\mathit{AC}=\mathit{AD}=\mathit{BE}=\mathit{BD}=\mathit{CE}$，求证：五边形 $\mathit{ABCDE}$是正五边形；

②如图2，若 $\mathit{AC}=\mathit{BE}=\mathit{CE}$，请判断五边形 $\mathit{ABCDE}$是不是正五边形，并说明理由：

（2）判断下列命题的真假．（在括号内填写“真”或“假” $)$

如图3，已知凸六边形 $\mathit{ABCDEF}$的各条边都相等．

①若 $\mathit{AC}=\mathit{CE}=\mathit{EA}$，则六边形 $\mathit{ABCDEF}$是正六边形； $($　　 $)$

②若 $\mathit{AD}=\mathit{BE}=\mathit{CF}$，则六边形 $\mathit{ABCDEF}$是正六边形． $($　　 $)$

如图，在平面直角坐标系中，正六边形 $\mathit{ABCDEF}$的对称中心 $P$在反比例函数 $y=\frac{k}{x}(k>0,x>0)$的图象上，边 $\mathit{CD}$在 $x$轴上，点 $B$在 $y$轴上，已知 $\mathit{CD}=2$．

（1）点 $A$是否在该反比例函数的图象上？请说明理由；

（2）若该反比例函数图象与 $\mathit{DE}$交于点 $Q$，求点 $Q$的横坐标；

（3）平移正六边形 $\mathit{ABCDEF}$，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．

下列图形为正多边形的是 $($ 　　 $)$

A．

B．

C．

D．

已知正方形 $\mathit{MNOK}$ 和正六边形 $\mathit{ABCDEF}$ 边长均为1，把正方形放在正六边形中，使 $\mathit{OK}$ 边与 $\mathit{AB}$ 边重合，如图所示，按下列步骤操作：

将正方形在正六边形中绕点 $B$ 顺时针旋转，使 $\mathit{KM}$ 边与 $\mathit{BC}$ 边重合，完成第一次旋转；再绕点 $C$ 顺时针旋转，使 $\mathit{MN}$ 边与 $\mathit{CD}$ 边重合，完成第二次旋转； $\dots$ 在这样连续6次旋转的过程中，点 $B$ ， $M$ 间的距离可能是 $($ 　　 $)$

A．

1.4

B．

1.1

C．

0.8

D．

0.5

如图为八个全等的正六边形（六条边相等，六个角相等）紧密排列在同一平面上的情形．根据图中标示的各点位置，下列三角形中与△ACD全等的是（）

A．△ACF

B．△AED

C．△ABC

D．△BCF

如图所示，把一张矩形纸片对折，折痕为AB，再把以AB的中点O为顶点的平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是（）

A．正三角形

B．正方形

C．正五边形

D．正六边形

下列说法正确的有 （）个①连接两点的线段叫两点之间的距离；②直线比线段长；③若AM=BM，则M为AB的中点；④由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形．

A．0

B．1

C．2

D．3