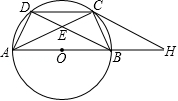
如图,点 A, B, C, D是直径为 AB的⊙ O上的四个点, C是劣弧 的中点, AC与 BD交于点 E.
(1)求证: DC 2= CE• AC;
(2)若 AE=2, EC=1,求证:△ AOD是正三角形;
(3)在(2)的条件下,过点 C作⊙ O的切线,交 AB的延长线于点 H,求△ ACH的面积.
已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.

如图,将 绕点 顺时针旋转 得到 ,点 的对应点 恰好落在 的延长线上,连接 .
(1)求证: ;
(2)若 , ,求 , 两点旋转所经过的路径长之和.

如图,将正 边形绕点 顺时针旋转 后,发现旋转前后两图形有另一交点 ,连接 ,我们称 为"叠弦";再将"叠弦" 所在的直线绕点 逆时针旋转 后,交旋转前的图形于点 ,连接 ,我们称 为"叠弦角", 为"叠弦三角形".
[探究证明]
(1)请在图1和图2中选择其中一个证明:"叠弦三角形" 是等边三角形;
(2)如图2,求证: .
[归纳猜想]
(3)图1、图2中的"叠弦角"的度数分别为 , ;
(4)图 中,"叠弦三角形" 等边三角形(填"是"或"不是"
(5)图 中,"叠弦角"的度数为 (用含 的式子表示)
