如图,在菱形 中, , ,点 是这个菱形内部或边上的一点.若以 , , 为顶点的三角形是等腰三角形,则 , , 两点不重合)两点间的最短距离为 .

经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段 是 的“和谐分割线”, 为等腰三角形, 和 相似, ,则 的度数为 .

阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边 中, 是 边上一点(不含端点 , , 是 的外角 的平分线上一点,且 .求证: .
点拨:如图②,作 , 与 的延长线相交于点 ,得等边 ,连接 .易证: ,可得 , ;又 ,则 ,可得 ;由 ,进一步可得 ,又因为 ,所以 ,即: .
问题:如图③,在正方形 中, 是 边上一点(不含端点 , , 是正方形 的外角 的平分线上一点,且 .求证: .

在▱ABCD中, ,AE平分 交BC于点E,DF平分∠ADC交BC于点F,且 ,则AB的长为( )
A.3B.5C.2或3D.3或5
如图,在四边形 ABCD中,∠ B=∠ C=90°, AB> CD, AD= AB+ CD.
(1)利用尺规作∠ ADC的平分线 DE,交 BC于点 E,连接 AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,
①证明: AE⊥ DE;
②若 CD=2, AB=4,点 M, N分别是 AE, AB上的动点,求 BM+ MN的最小值.

在▱ ABCD中, AE平分∠ BAD交边 BC于 E, DF平分∠ ADC交边 BC于 F,若 AD=11, EF=5,则 AB= .
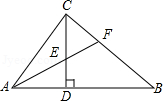
如图,在Rt△ ABC中,∠ ACB=90°, CD⊥ AB,垂足为 D, AF平分∠ CAB,交 CD于点 E,交 CB于点 F.若 AC=3, AB=5,则 CE的长为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知线段  ,分别以
,分别以  、
、  为圆心,大于
AB为半径作弧,连接弧的交点得到直线
为圆心,大于
AB为半径作弧,连接弧的交点得到直线  ,在直线
,在直线  上取一点
上取一点  ,使得
,使得  ,延长
,延长  至
至  ,求
,求  的度数为
的度数为 


| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )

A.150°B.130°C.120°D.100°