"三等分角"大约是在公元前五世纪由古希腊人提出来的,借助如图所示的"三等分角仪"能三等分任一角.这个三等分角仪由两根有槽的棒 , 组成,两根棒在 点相连并可绕 转动、 点固定, ,点 、 可在槽中滑动.若 ,则 的度数是
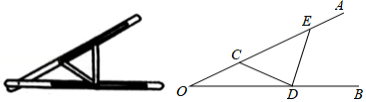
| A. |
|
B. |
|
C. |
|
D. |
|
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在中,
,
是
的角平分线,
,
分别是
,
上的点.
求证:四边形是邻余四边形.
(2)如图2,在的方格纸中,
,
在格点上,请画出一个符合条件的邻余四边形
,使
是邻余线,
,
在格点上.
(3)如图3,在(1)的条件下,取中点
,连结
并延长交
于点
,延长
交
于点
.若
为
的中点,
,
,求邻余线
的长.

如图,在中,
.
(1)已知线段的垂直平分线与
边交于点
,连接
,求证:
.
(2)以点为圆心,线段
的长为半径画弧,与
边交于点
,连接
.若
,求
的度数.

如图,在中,
,
于点
.
(1)若,求
的度数;
(2)若点在边
上,
交
的延长线于点
.求证:
.

如图, 是 的直径, 是 的切线, 为切点, 与 交于点 ,连结 .若 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,是以
为底的等腰三角形,
是边
上的高,点
、
分别是
、
的中点.
(1)求证:四边形是菱形;
(2)如果四边形的周长为12,两条对角线的和等于7,求四边形
的面积
.

如图, 、 是 上的两点, 的垂直平分线与 交于 、 两点,与线段 交于 点.若 ,则
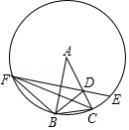
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在中,
,点
在
上,以
为半径作
,与
相交于点
,与
相切于点
,过点
作
,垂足为
.
(1)求证:是
的切线;
(2)若,
,求
的半径.

如图,在中,
,
是
的中点,
与
相切于点
,
交
于点
(1)求证:是
的切线;
(2)若,点
是
上一个动点(不与
,
两点重合),求
的度数.

等腰三角形的两边分别为3和6,则这个三角形的周长是
| A. |
9 |
B. |
12 |
C. |
15 |
D. |
12或15 |
已知,
分别与
相切于点
,
,
,
为
上一点.
(Ⅰ)如图①,求的大小;
(Ⅱ)如图②,为
的直径,
与
相交于点
.若
,求
的大小.

如图,将 绕点 顺时针旋转得到 ,使点 的对应点 恰好落在边 上,点 的对应点为 ,连接 ,下列结论一定正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
已知是
的直径,
是
的切线,
,
交
于点
,
是
上一点,延长
交
于点
.
(1)如图①,求和
的大小;
(2)如图②,当时,求
的大小.
