初中数学等腰三角形的性质试题

操作题：如图，△ABC内接于⊙O，AB=AC，P是⊙O上一点．

（1）请你只用无刻度的直尺，分别画出图①和图②中∠P的平分线；
（2）结合图②，说明你这样画的理由．

等腰三角形中，已知两边的长分别是9和5，则周长为__________．

如图，在四边形ABCD中，点E、F是BC、CD的中点，且AE⊥BC，AF⊥CD．

（1）求证：AB=AD．
（2）请你探究∠EAF，∠BAE，∠DAF之间有什么数量关系？并证明你的结论．

如图：已知在中，∠ACB=90°，∠BAC=36°，在直线上找点,使是等腰三角形，则的度数为             ．

如图，等腰，，，于点，点是延长线上一点，点是线段上一点，，下面结论：
①；
②是等边三角形；
③；
④．
其中正确的是（  ）

A．②③

B．①②④

C．③④

D．①②③④

如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，则∠BCE的度数是         ．

如图，已知AB是⊙O的直径，∠AOE=60°，点C是AB延长线上一点，CE交⊙O于点D，且CD=OB，则∠C等于（  ）

A．10°

B．15°

C．20°

D．30°

（年青海省中考）如图，点O为所在圆的圆心，∠BOC=112°，点D在BA的延长线上，AD=AC，则∠D=          ．

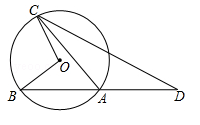
（年贵州省铜仁市）如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．

（1）求证：CB平分∠ACE；
（2）若BE=3，CE=4，求⊙O的半径．

（年青海省西宁市）等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是           ．

（年贵州省毕节）等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为        ．

（年新疆乌鲁木齐市）等腰三角形的一个外角是60°，则它的顶角的度数是            ．

（年贵州省毕节）等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为        ．

（年青海省中考）一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角形的斜边上，AC与DM，DN分别交于点E，F，把△DEF绕点D旋转到一定位置，使得DE=DF，则∠BDN的度数是（ ）

A．105°

B．115°

C．120°

D．135°

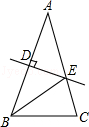
（年贵州省毕节）如图，已知D为△ABC边AB的中点，E在AC上，将△ABC沿着DE折叠，使A点落在BC上的F处．若∠B=65°，则∠BDF等于（ ）

A．65°

B．50°

C．60°

D．57．5°