如图,正方形 中, 为 中点, , , 交 于 ,则 的度数为

A. B. C. D.
如图,正方形 中, ,点 在边 上,且 .将 沿 对折至 ,延长 交边 于点 ,连接 、 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是

A.2B.3C.4D.5
如图,矩形 绕点 逆时针旋转 后得到矩形 , 与 交于点 ,延长 交 于 ,若 , ,则 的长度为

A. B. C. D.
如图,在等腰直角 中, ,点 是 的中点,且 ,将一块直角三角板的直角顶点放在点 处,始终保持该直角三角板的两直角边分别与 、 相交,交点分别为 、 ,则

A. B. C.2D.
如图,在边长为4的正方形 中, 、 是 边上的两个动点,且 ,连接 、 、 , 与 交于点 ,连接 交 于点 ,连接 ,下列结论正确的个数是
① ② 平分 ③ ④ ⑤线段 的最小值是 .

A.2B.3C.4D.5
如图,在正方形 中,点 , 分别在边 , 上, 、 分别交 于点 , ,连接 、 ,且 .下列结论:① , ;② ;③ ;④ ;⑤图中只有4对相似三角形.其中正确结论的个数是

A.5B.4C.3D.2
如图, , ,动点 从点 出发,沿射线 方向移动,以 为边在右侧作等边 ,连接 ,则 所在直线与 所在直线的位置关系是

A.平行B.相交
C.垂直D.平行、相交或垂直
如图,在正方形 中,点 , 分别在 , 上, ,则图中与 相等的角的个数是

A.1B.2C.3D.4
如图, 是正方形 的边 的中点,点 与 关于 对称, 的延长线与 交于点 ,与 的延长线交于点 ,点 在 的延长线上,作正方形 ,连接 ,记正方形 , 的面积分别为 , ,则下列结论错误的是

A. B. C. D.
如图,在正方形 中, 是对角线 与 的交点, 是 边上的动点(点 不与 , 重合), , 与 交于点 ,连接 , , .下列五个结论:① ;② ;③ ;④ ;⑤若 ,则 的最小值是 ,其中正确结论的个数是
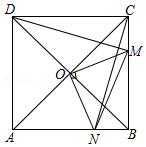
A.2B.3C.4D.5
如图,边长为 的正方形 的对角线 与 交于点 ,将正方形 沿直线 折叠,点 落在对角线 上的点 处,折痕 交 于点 ,则

A. B. C. D.
如图,矩形 中, , , 且 与 之间的距离为3,则 的长是
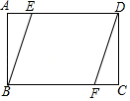
A. B. C. D.
如图,矩形 中, 为 中点,过点 的直线分别与 、 交于点 、 ,连接 交 于点 ,连接 、 .若 , ,则下列结论:① 垂直平分 ;② ;③ ;④ .其中正确结论的个数是

A.4个B.3个C.2个D.1个
如图,四边形 是菱形, , ,扇形 的半径为2,圆心角为 ,则图中阴影部分的面积是

A. B. C. D.