初中数学三角形的面积试题

下面有4张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长都是1，请在方格纸中分别画出符合要求的图形，所画图形各顶点必须与方格纸中小正方形的顶点重合，具体要求如下：

（1）画一个直角边长为4，面积为6的直角三角形．

（2）画一个底边长为4，面积为8的等腰三角形．

（3）画一个面积为5的等腰直角三角形．

（4）画一个一边长为 $2\sqrt{2}$，面积为6的等腰三角形．

如图，四边形 $\mathit{ABCD}$中， $\angle A=\angle C=90°$， $\angle B=60°$， $\mathit{AD}=1$， $\mathit{BC}=2$，则四边形 $\mathit{ABCD}$的面积是 $($　　 $)$

A． $\frac{3\sqrt{3}}{2}$B．3C． $2\sqrt{3}$D．4

如图，已知 $\mathit{\Delta ABC}$中， $\angle C=90°$，点 $M$从点 $C$出发沿 $\mathit{CB}$方向以 $1\mathit{cm}/s$的速度匀速运动，到达点 $B$停止运动，在点 $M$的运动过程中，过点 $M$作直线 $\mathit{MN}$交 $\mathit{AC}$于点 $N$，且保持 $\angle \mathit{NMC}=45°$，再过点 $N$作 $\mathit{AC}$的垂线交 $\mathit{AB}$于点 $F$，连接 $\mathit{MF}$．将 $\mathit{\Delta MNF}$关于直线 $\mathit{NF}$对称后得到 $\mathit{\Delta ENF}$，已知 $\mathit{AC}=8\mathit{cm}$， $\mathit{BC}=4\mathit{cm}$，设点 $M$运动时间为 $t\left(s\right)$， $\mathit{\Delta ENF}$与 $\mathit{\Delta ANF}$重叠部分的面积为 $y\left(c{m}^2\right)$．

（1）在点 $M$的运动过程中，能否使得四边形 $\mathit{MNEF}$为正方形？如果能，求出相应的 $t$值；如果不能，说明理由；

（2）求 $y$关于 $t$的函数解析式及相应 $t$的取值范围；

（3）当 $y$取最大值时，求 $\sin \angle \mathit{NEF}$的值．

已知三角形的三边长分别为 $a$、 $b$、 $c$，求其面积问题，中外数学家曾经进行过深入研究，古希腊的几何学家海伦 $(\mathit{Heron}$，约公元50年）给出求其面积的海伦公式 $S=\sqrt{p(p-a)(p-b)(p-c)}$，其中 $p=\frac{a+b+c}{2}$；我国南宋时期数学家秦九韶（约 $1202-1261)$曾提出利用三角形的三边求其面积的秦九韶公式 $S=\frac{1}{2}\sqrt{a^2{b}^2-{\left(\frac{a^2+b^2-c^2}{2}\right)}^2}$，若一个三角形的三边长分别为2，3，4，则其面积是 $($　　 $)$

A． $\frac{3\sqrt{15}}{8}$B． $\frac{3\sqrt{15}}{4}$C． $\frac{3\sqrt{15}}{2}$D． $\frac{\sqrt{15}}{2}$

我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为 $a$， $b$， $c$，则该三角形的面积为 $S=\sqrt{\frac{1}{4}[a^2{b}^2-{\left(\frac{a^2+b^2-c^2}{2}\right)}^2]}$．现已知 $\mathit{\Delta ABC}$的三边长分别为1，2， $\sqrt{5}$，则 $\mathit{\Delta ABC}$的面积为　　．

点 $A$、 $B$、 $C$在格点图中的位置如图所示，格点小正方形的边长为1，则点 $C$到线段 $\mathit{AB}$所在直线的距离是　　．

如图，在 $\mathit{\Delta ABC}$中，点 $D$是边 $\mathit{BC}$的中点，连结 $\mathit{AD}$并延长到点 $E$，使 $\mathit{DE}=\mathit{AD}$，连结 $\mathit{CE}$．

（1）求证： $\mathit{\Delta ABD}\cong \mathit{\Delta ECD}$；

（2）若 $\mathit{\Delta ABD}$的面积为5，求 $\mathit{\Delta ACE}$的面积．

如图， $\mathit{AC}\perp x$轴于点 $A$，点 $B$在 $y$轴的正半轴上， $\angle \mathit{ABC}=60°$， $\mathit{AB}=4$， $\mathit{BC}=2\sqrt{3}$，点 $D$为 $\mathit{AC}$与反比例函数 $y=\frac{k}{x}$的图象的交点 ． 若直线 $\mathit{BD}$将 $\mathit{\Delta ABC}$的面积分成 $1:2$的两部分， 则 $k$的值为　        ．

如图， $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}=2$， $\angle B=30°$， $\mathit{\Delta ABC}$绕点 $A$逆时针旋转 $\alpha (0°<\alpha <120°)$得到△ $\mathit{AB}\text{'}C\text{'}$， $B\text{'}C\text{'}$与 $\mathit{BC}$， $\mathit{AC}$分别交于点 $D$， $E$．设 $\mathit{CD}+\mathit{DE}=x$， $\mathit{\Delta AEC}\text{'}$的面积为 $y$，则 $y$与 $x$的函数图象大致 $($　　 $)$

A．

B．

C．

D．

如图， $\odot O$的半径 $\mathit{OD}$垂直于弦 $\mathit{AB}$，垂足为点 $C$，连接 $\mathit{AO}$并延长交 $\odot O$于点 $E$，连接 $\mathit{BE}$， $\mathit{CE}$．若 $\mathit{AB}=8$， $\mathit{CD}=2$，则 $\mathit{\Delta BCE}$的面积为 $($　　 $)$

A．12B．15C．16D．18

如图， $\text{Rt}\Delta \text{ABC}$中， $\angle A=30°$， $\angle \mathit{ABC}=90°$．将 $\text{Rt}\Delta \text{ABC}$绕点 $B$逆时针方向旋转得到△ $A^{\text{'}}B{C}^{\text{'}}$．此时恰好点 $C$在 $A^{\text{'}}{C}^{\text{'}}$上， $A^{\text{'}}B$交 $\mathit{AC}$于点 $E$，则 $\mathit{\Delta ABE}$与 $\mathit{\Delta ABC}$的面积之比为 $($　　 $)$

A． $\frac{1}{3}$B． $\frac{1}{2}$C． $\frac{2}{3}$D． $\frac{3}{4}$

如图， $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$， $\mathit{BC}=6$， $\mathit{AC}=8$， $D$、 $E$分别为 $\mathit{AC}$、 $\mathit{AB}$的中点，连接 $\mathit{DE}$，则 $\mathit{\Delta ADE}$的面积是　．

如图，平行四边形 $\mathit{ABCD}$的对角线 $\mathit{AC}$、 $\mathit{BD}$相交于点 $O$， $\mathit{AE}$平分 $\angle \mathit{BAD}$，分别交 $\mathit{BC}$、 $\mathit{BD}$于点 $E$、 $P$，连接 $\mathit{OE}$， $\angle \mathit{ADC}=60°$， $\mathit{AB}=\frac{1}{2}\mathit{BC}=1$，则下列结论：

① $\angle \mathit{CAD}=30°$② $\mathit{BD}=\sqrt{7}$③ $S_{\mathit{平行四边形ABCD}}=\mathit{AB}\cdot \mathit{AC}$④ $\mathit{OE}=\frac{1}{4}\mathit{AD}$⑤ $S_{\mathit{\Delta APO}}=\frac{\sqrt{3}}{12}$，正确的个数是 $($　　 $)$

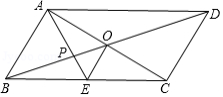
A．2B．3C．4D．5

如图，四边形 $\mathit{ABCD}$中， $\mathit{AB}=\mathit{AD}$， $\mathit{AC}=5$， $\angle \mathit{DAB}=\angle \mathit{DCB}=90°$，则四边形 $\mathit{ABCD}$的面积为 $($　　 $)$

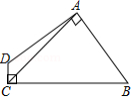
A．15B．12.5C．14.5D．17

$\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ABC}=90°$， $\mathit{AB}=3$， $\mathit{BC}=4$，过点 $B$的直线把 $\mathit{\Delta ABC}$分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是　　．