如图,在 中, , 是 的中点,过点 作 的平行线交 于点 ,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为

A. B.5C. D.10
如图,在平面直角坐标系中,矩形 的对角线 的中点与坐标原点重合,点 是 轴上一点,连接 .若 平分 ,反比例函数 的图象经过 上的两点 , ,且 , 的面积为18,则 的值为

A.6B.12C.18D.24
如图,三角形纸片 ,点 是 边上一点,连接 ,把 沿着 翻折,得到 , 与 交于点 ,连接 交 于点 .若 , , , 的面积为2,则点 到 的距离为

A. B. C. D.
如图,在 的网格中,每个小正方形的边长均为1,点 , , 都在格点上,若 是 的高,则 的长为

A. B. C. D.
在 中, , 交 的延长线于点 .

特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为 ,一条直角边与 重合,另一条直角边恰好经过点 .通过观察、测量 与 的长度,得到 .请给予证明.
猜想论证:
(2)当三角尺沿 方向移动到图2所示的位置时,一条直角边仍与 边重合,另一条直角边交 于点 ,过点 作 垂足为 .此时请你通过观察、测量 、 与 的长度,猜想并写出 、 与 之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿 方向继续移动到图3所示的位置(点 在线段 上,且点 与点 不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
如图,在矩形 中, ,点 在边 上,连接 ,以 为边向右上方作正方形 ,作 ,垂足为 ,连接 .
(1)求证: ;
(2)当 为何值时, 的面积最大?
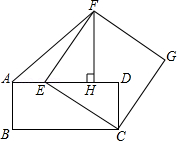
如图,平面直角坐标系中,已知点 的坐标为 .
(1)请用直尺(不带刻度)和圆规作一条直线 ,它与 轴和 轴的正半轴分别交于点 和点 ,且使 , 与 的面积相等.(作图不必写作法,但要保留作图痕迹.
(2)问:(1)中这样的直线 是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线 ,并写出与之对应的函数表达式.
如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .

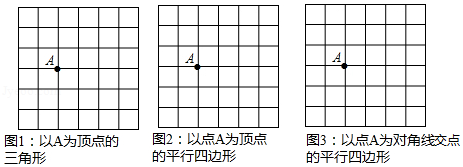
如图,在 的网格中,每个小正方形的边长为1,点 在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
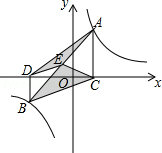
如图,点 , 在反比例函数 的图象上, 轴, 轴,垂足 , 分别在 轴的正、负半轴上, ,已知 , 是 的中点,且 的面积是 的面积的2倍,则 的值是 .
下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个一边长为 ,面积为6的等腰三角形.
