等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ,其内切圆的半径长为 ;
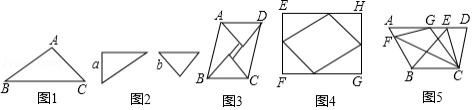
(2)①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ;(结果用含 的式子表示)

②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: ,
(3)①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ;(结果保留
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造,若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.

如图,已知 中, ,点 从点 出发沿 方向以 的速度匀速运动,到达点 停止运动,在点 的运动过程中,过点 作直线 交 于点 ,且保持 ,再过点 作 的垂线交 于点 ,连接 .将 关于直线 对称后得到 ,已知 , ,设点 运动时间为 , 与 重叠部分的面积为 .
(1)在点 的运动过程中,能否使得四边形 为正方形?如果能,求出相应的 值;如果不能,说明理由;
(2)求 关于 的函数解析式及相应 的取值范围;
(3)当 取最大值时,求 的值.

(回顾)
如图1, 中, , , ,则 的面积等于 .
(探究)
图2是同学们熟悉的一副三角尺,一个含有 的角,较短的直角边长为 ;另一个含有 的角,直角边长为 ,小明用两副这样的三角尺拼成一个平行四边形 (如图 ,用了两种不同的方法计算它的面积,从而推出 ,小丽用两副这样的三角尺拼成了一个矩形 (如图 ,也推出 ,请你写出小明或小丽推出 的具体说理过程.
(应用)
在四边形 中, , , , , (如图5)
(1)点 在 上,设 ,求 的最小值;
(2)点 在 上,将 沿 翻折,点 落在 上的点 处,点 是 的中点吗?说明理由.
问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

已知等边三角形ABC的边长为2.
(1)如图一,若 ,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若 ,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点 ,E是DC上的一点,连接ME,ME与AD交于点O,且 .
①求证:ME是△ABC的面径;
②连接AE,求证: ;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)