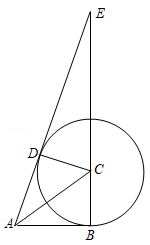
如图,在 中, ,以点 为圆心, 为半径的圆交 于点 ,点 在边 上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)已知 , ,求 的半径.

如图,点 、 在反比例函数 的图象上,延长 交 轴于 点,若 的面积是12,且点 是 的中点,则 .

如图,在 中, , ,点 、 在 上,边 、 分别交 于 、 两点,点 是 的中点,则 .

《九章算术》中一道"引葭赴岸"问题:"今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?"题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面部分 为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 恰好碰到岸边的 处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.

如图,折叠矩形纸片 ,使点 落在点 处,折痕为 ,已知 , ,则 的长是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 .
(1)求证: ;
(2)若 , , ,求 的值.

如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为 (结果保留根号)

如图, 与 交于点 , , , 为 延长线上一点,过点 作 ,交 的延长线于点 .
(1)求证 ;
(2)若 , , ,求 的长.

如图, 中, ,以点 为圆心, 为半径作 , 为 上一点,连接 、 , , 平分 .
(1)求证: 是 的切线;
(2)延长 、 相交于点 ,若 ,求 的值.
如图, 、 、 、 是直线 上的四点, , , .
(1)求证: ;
(2)将 沿直线 翻折得到△ .
①用直尺和圆规在图中作出△ (保留作图痕迹,不要求写作法);
②连接 ,则直线 与 的位置关系是 .

如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .
