如图,在 中, , , , , 分别为 , , 的中点,若 ,则 的长度为

A. B.1C. D.
现有长分别为1,2,3,4,5的木条各一根,从这5根木条中任取3根,能构成三角形的概率是 .
如图, 和 都是等腰直角三角形, , , 的顶点 在 的斜边 上,若 , ,则两个三角形重叠部分的面积为

A. B. C. D.
如图①,在四边形 中, 于点 , ,点 为 中点, 为线段 上的点,且 .
(1)求证: 平分 ;
(2)若 ,连接 ,当四边形 为平行四边形时,求线段 的长;
(3)如图②,若点 为 的中点,连接 、 ,求证: .

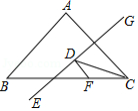
如图,在 中, , 于点 , 为 的中点,连接 、 ,下列结论:① ;② ;③ ;④ ,其中正确结论的个数共有

A.1个B.2个C.3个D.4个
将一副直角三角板按如图所示的位置放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边放在同一条直线上,则 的度数是
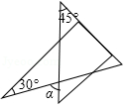
A. B. C. D.
如图,等腰 的底边 ,面积为120,点 在边 上,且 , 是腰 的垂直平分线,若点 在 上运动,则 周长的最小值为 .
如图,正方形 中, , 分别在边 , 上, , 相交于点 ,若 , ,则 的值是
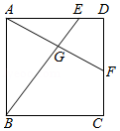
A. B. C. D.
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为 ,较短直角边长为 .若 ,大正方形的面积为25,则小正方形的边长为

A.9B.6C.4D.3
如图, 的对角线 , 相交于点 , 是 中点,且 ,则 的周长为

A.20B.16C.12D.8
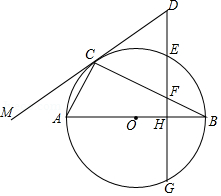
已知: 内接于 , 是 的直径,作 于 ,交 于 ,延长 交直线 于 ,且 ,求证:
(1) 是 的切线;
(2) 是等腰三角形.