初中数学点到直线的距离试题

如图， $\angle \mathit{AOB}=60°$，点 $P$为射线 $\mathit{OA}$上的一动点．过点 $P$作 $\mathit{PC}\perp \mathit{OB}$于点 $C$．点 $D$在 $\angle \mathit{AOB}$内，且满足 $\angle \mathit{APD}=\angle \mathit{OPC}$， $\mathit{DP}+\mathit{PC}=10$．

（1）当 $\mathit{PC}=6$时，求点 $D$到 $\mathit{OB}$的距离；

（2）在射线 $\mathit{OA}$上是否存在一定点 $M$，使得 $\mathit{MD}=\mathit{MC}$？若存在，请用直尺（不带刻度）和圆规作出点 $M$（不必写作法，但要保留作图痕迹），并求 $\mathit{OM}$的长；若不存在，说明理由．

如图， $\mathit{AB}\perp \mathit{AC}$， $\mathit{AD}\perp \mathit{BC}$，垂足分别为 $A$， $D$，则图中能表示点到直线距离的线段共有 $($　　 $)$

A．2条B．3条C．4条D．5条

已知点 $P(x_0$， $y_0)$和直线 $y=\mathit{kx}+b$，则点 $P$到直线 $y=\mathit{kx}+b$的距离证明可用公式 $d=\frac{|k{x}_0-y_0+b|}{\sqrt{1+k^2}}$计算．

例如：求点 $P(-1,2)$到直线 $y=3x+7$的距离．

解：因为直线 $y=3x+7$，其中 $k=3$， $b=7$．

所以点 $P(-1,2)$到直线 $y=3x+7$的距离为： $d=\frac{|k{x}_0-y_0+b|}{\sqrt{1+k^2}}=\frac{|3\times (-1)-2+7|}{\sqrt{1+3^2}}=\frac{2}{\sqrt{10}}=\frac{\sqrt{10}}{5}$．

根据以上材料，解答下列问题：

（1）求点 $P(1,-1)$到直线 $y=x-1$的距离；

（2）已知 $\odot Q$的圆心 $Q$坐标为 $(0,5)$，半径 $r$为2，判断 $\odot Q$与直线 $y=\sqrt{3}x+9$的位置关系并说明理由；

（3）已知直线 $y=-2x+4$与 $y=-2x-6$平行，求这两条直线之间的距离．

阅读理解题

在平面直角坐标系 $\mathit{xOy}$中，点 $P(x_0$， $y_0)$到直线 $\mathit{Ax}+\mathit{By}+C=0(A^2+B^2\ne 0)$的距离公式为： $d=\frac{|A{x}_0+B{y}_0+C|}{\sqrt{A^2+B^2}}$，

例如，求点 $P(1,3)$到直线 $4x+3y-3=0$的距离．

解：由直线 $4x+3y-3=0$知： $A=4$， $B=3$， $C=-3$

所以 $P(1,3)$到直线 $4x+3y-3=0$的距离为： $d=\frac{|4\times 1+3\times 3-3|}{\sqrt{4^2+3^2}}=2$

根据以上材料，解决下列问题：

（1）求点 $P_1(0,0)$到直线 $3x-4y-5=0$的距离．

（2）若点 $P_2(1,0)$到直线 $x+y+C=0$的距离为 $\sqrt{2}$，求实数 $C$的值．

如图，经过直线 $l$外一点画 $l$的垂线，能画出 $($　　 $)$

A．1条B．2条C．3条D．4条

如图，四边形 $\mathit{ABCD}$中， $\angle \mathit{BAD}=\angle \mathit{ADC}=90°$， $\mathit{AB}=\mathit{AD}=3\sqrt{2}$， $\mathit{CD}=2\sqrt{2}$，点 $P$是四边形 $\mathit{ABCD}$四条边上的一个动点，若 $P$到 $\mathit{BD}$的距离为 $\frac{5}{2}$，则满足条件的点 $P$有　　个．

如图，点 A， B， C在直线 l上， PB⊥ l， PA＝6 cm， PB＝5 cm， PC＝7 cm，则点 P到直线 l的距离是 　　 cm．

已知点 $P(x_0$ ， $y_0)$ 和直线 $y=\mathit{kx}+b$ ，求点 $P$ 到直线 $y=\mathit{kx}+b$ 的距离 $d$ 可用公式 $d=\frac{|k{x}_0-y_0+b|}{\sqrt{1+k^2}}$ 计算．根据以上材料解决下面问题：如图， $\odot C$ 的圆心 $C$ 的坐标为 $(1,1)$ ，半径为1，直线 $l$ 的表达式为 $y=-2x+6$ ， $P$ 是直线 $l$ 上的动点， $Q$ 是 $\odot C$ 上的动点，则 $\mathit{PQ}$ 的最小值是 $($ 　　 $)$

A．

$\frac{3\sqrt{5}}{5}$

B．

$\frac{3\sqrt{5}}{5}-1$

C．

$\frac{6\sqrt{5}}{5}-1$

D．

2

在平面直角坐标系中，点，到直线的距离公式为：，则点到直线的距离为　　．

下列说法正确的是（　　）

A．	有两边和一角分别相等的两个三角形全等
B．	有一组对边平行，且对角线相等的四边形是矩形
C．	如果一个角的补角等于它本身，那么这个角等于45°
D．	点到直线的距离就是该点到该直线的垂线段的长度

已知点，到直线的距离可表示为，例如：点到直线的距离．据此进一步可得两条平行线和之间的距离为　　．

如图，是的内接三角形，且是的直径，点为上的动点，且，的半径为6，则点到距离的最大值是　　．

如图所示，点 $P$ 到直线 $l$ 的距离是 $($ 　　 $)$

A．

线段 $\mathit{PA}$ 的长度

B．

线段 $\mathit{PB}$ 的长度

C．

线段 $\mathit{PC}$ 的长度

D．

线段 $\mathit{PD}$ 的长度

如图，由相同边长的小正方形组成的网格图形，A、B、C都在格点上．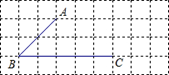

（1）在网格内过点C画与线段AB平行且相等的线段CD；
（2）过点A画直线BC的垂线，并注明垂足为点G；过点A画直线AB的垂线，交BC于点H．
（3）线段AH的长度是点到直线的距离，点A到直线BC的距离是．
（4）线段AG、AH的大小关系为：AG、AH（填“>”或“<”或“=”），理由是．

如图，BC⊥AC，CB=8cm，AC=6cm，AB=10cm，那么点B到AC的距离是         cm，点A到BC的距离是        cm，C到AB的距离是               cm．