四位同学在研究函数 , 是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, ,已知这四位同学中只有一位发现的结论是错误的,则该同学是
A.甲B.乙C.丙D.丁
抛物线 (其中 , 是常数)过点 ,且抛物线的对称轴与线段 有交点,则 的值不可能是
A.4B.6C.8D.10
如图,二次函数 的图象与 轴交于 , 两点,与 轴正半轴交于点 ,它的对称轴为直线 .则下列选项中正确的是
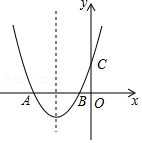
A. B.
C. D.当 为实数)时,
在平面直角坐标系中,点 为坐标原点,抛物线 与 轴交于点 ,与 轴正半轴交于点 ,连接 ,将 向右上方平移,得到 △ ,且点 , 落在抛物线的对称轴上,点 落在抛物线上,则直线 的表达式为
A. B. C. D.
函数 与函数 的图象如图所示,有以下结论:① ;② ;③ ;④方程组 的解为 , ;⑤当 时, .其中正确的是
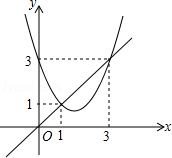
A.①②③B.②③④C.③④⑤D.②③⑤
如图,已知抛物线 的图象与 轴交于 、 两点,其对称轴与 轴交于点 ,其中 、 两点的横坐标分别为 和1,下列说法错误的是

A. B.
C. D.当 时, 随 的增大而减小
矩形 的两条对称轴为坐标轴,点 的坐标为 ,一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点 重合,此时抛物线的函数表达式为 ,再次平移透明纸,使这个点与点 重合,则该抛物线的函数表达式变为
A. B. C. D.
已知二次函数 的图象如图所示,有下列结论:① ;② ;③ ;④不等式 的解集为 ,正确的结论个数是
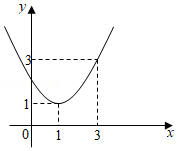
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
若用“ ”表示一种运算规则,我们规定: ,如: .以下说法中错误的是
A.不等式 的解集是
B.函数 的图象与 轴有两个交点
C.在实数范围内,无论 取何值,代数式 的值总为正数
D.方程 的解是
在平面直角坐标系中,已知函数 , , ,其中 , , 是正实数,且满足 .设函数 , , 的图象与 轴的交点个数分别为 , , ,
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
二次函数 的图象如图所示,则下列结论中不正确的是

| A. |
|
B. |
函数的最大值为 |
| C. |
当 时, |
D. |
|
已知函数 ,则下列说法不正确的个数是
①若该函数图像与 轴只有一个交点,则 ;
②方程 至少有一个整数根;
③若 ,则 的函数值都是负数;
④不存在实数 ,使得 对任意实数 都成立.
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
已知抛物线 , , 是常数, , 经过点 ,其对称轴是直线 .有下列结论:
① ;
②关于 的方程 有两个不等的实数根;
③ .
其中,正确结论的个数是
A.0B.1C.2D.3