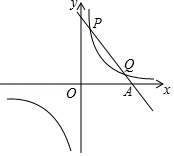
已知一次函数y=k1x+b与反比例函数 的图象交于第一象限内的P( ,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
小明根据学习函数的经验,参照研究函数的过程与方法,对函数 的图象与性质进行探究.
因为 ,即 ,所以可以对比函数 来探究.
列表:(1)下表列出 与 的几组对应值,请写出 , 的值: , ;
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
0 |
|
|
|
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示:

(2)请把 轴左边各点和右边各点,分别用条光滑曲线顺次连接起来;
(3)观察图象并分析表格,回答下列问题:
①当 时, 随 的增大而 ;(填“增大”或“减小”
②函数 的图象是由 的图象向 平移 个单位而得到.
③函数图象关于点 中心对称.(填点的坐标)
若点 A(﹣1, y 1), B(2, y 2), C(3, y 3)在反比例函数 y= 的图象上,则 y 1, y 2, y 3的大小关系是( )
| A. |
y 3<y 2<y 1 |
B. |
y 2<y 1<y 3 |
C. |
y 1<y 3<y 2 |
D. |
y 1<y 2<y 3 |
如图, 的三个顶点分别为 , , .若反比例函数 在第一象限内的图象与 有交点,则 的取值范围是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知点A(1,2)是反比例函数 图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 .

如图,在平面直角坐标系 中,已知直线 分别交反比例函数 和 在第一象限的图象于点 , ,过点 作 轴于点 ,交 的图象于点 ,连接 .若 是等腰三角形,则 的值是 .

已知反比例函数 ,下列结论:①图象必经过 ;②图象在二,四象限内;③ 随 的增大而增大;④当 时,则 .其中错误的结论有 个
A.3B.2C.1D.0
在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 , 称为点 的"倒数点".如图,矩形 的顶点 为 ,顶点 在 轴上,函数 的图象与 交于点 .若点 是点 的"倒数点",且点 在矩形 的一边上,则 的面积为 .

已知三个点 , , , , , 在反比例函数 的图象上,其中 ,下列结论中正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
已知反比例函数 的图象经过点 .
(1)求该反比例函数的表达式;
(2)如图,在反比例函数 的图象上点 的右侧取点 ,过点 作 轴的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 .
①过点 ,点 分别作 轴, 轴的垂线,两线相交于点 ,求证: , , 三点共线;
②若 ,求证: .
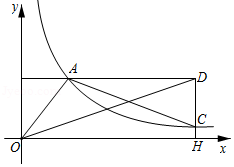
如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)求反比例函数的解析式;
(2)求 的面积.
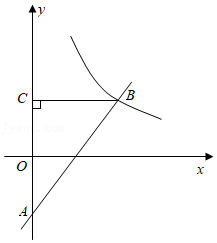
如图,在平面直角坐标系中,矩形 的对角线 的中点与坐标原点重合,点 是 轴上一点,连接 .若 平分 ,反比例函数 的图象经过 上的两点 , ,且 , 的面积为18,则 的值为

A.6B.12C.18D.24
探究函数 与 的相关性质.
(1)小聪同学对函数 进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
(2)请用配方法求函数 的最小值;
(3)猜想函数 的最小值为 .
