用纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为为非负整数).
(1)根据题意,填写下表:
一次复印页数(页 |
5 |
10 |
20 |
30 |
|
甲复印店收费(元 |
0.5 |
|
2 |
|
|
乙复印店收费(元 |
0.6 |
|
2.4 |
|
(2)设在甲复印店复印收费元,在乙复印店复印收费
元,分别写出
,
关于
的函数关系式;
(3)当时,顾客在哪家复印店复印花费少?请说明理由.
公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车 辆 为非负整数),试填写表格.
表一:
| 租用甲种货车的数量 辆 |
3 |
7 |
|
| 租用的甲种货车最多运送机器的数量 台 |
135 |
|
|
| 租用的乙种货车最多运送机器的数量 台 |
150 |
|
|
表二:
| 租用甲种货车的数量 辆 |
3 |
7 |
|
| 租用甲种货车的费用 元 |
|
2800 |
|
| 租用乙种货车的费用 元 |
|
280 |
|
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为次,选择方式一的总费用为
(元
,选择方式二的总费用为
(元
.
(1)请分别写出,
与
之间的函数表达式.
(2)小亮一年内在此游泳馆游泳的次数在什么范围时,选择方式一比方式二省钱.
我省某苹果基地销售优质苹果,该基地对需要送货且购买量在 (含 和 的客户有两种销售方案(客户只能选择其中一种方案)
方案 :每千克5.8元,由基地免费送货.
方案 :每千克5元,客户需支付运费2000元.
(1)请分别写出按方案 ,方案 购买这种苹果的应付款 (元 与购买量 之间的函数表达式;
(2)求购买量 在什么范围时,选用方案 比方案 付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

一辆汽车在某次行驶过程中,油箱中的剩余油量(升
与行驶路程
(千米)之间是一次函数关系,其部分图象如图所示.
(1)求关于
的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用(元
与绿化面积
(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500 元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.
(1)求如图所示的与
的函数解析式:(不要求写出定义域);
(2)如果某学校目前的绿化面积是1200平方米,试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.

某物流公司引进、
两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,
种机器人于某日0时开始搬运,过了1小时,
种机器人也开始搬运,如图,线段
表示
种机器人的搬运量
(千克)与时间
(时
的函数图象,线段
表示
种机器人的搬运量
(千克)与时间
(时
的函数图象.根据图象提供的信息,解答下列问题:
(1)求关于
的函数解析式;
(2)如果、
两种机器人连续搬运5个小时,那么
种机器人比
种机器人多搬运了多少千克?

根据记录,从地面向上以内,每升高
,气温降低
;又知在距离地面
以上高空,气温几乎不变.若地面气温为
,设距地面的高度为
处的气温为
(1)写出距地面的高度在以内的
与
之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为时,飞机距离地面的高度为
,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面
的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面
时,飞机外的气温.
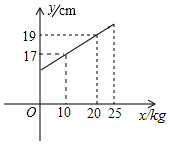
在所挂物体质量不超过时,一弹簧的长度
是所挂物体质量
的一次函数,其图象如图所示.
(1)求与
之间的函数表达式及该弹簧不挂物体时的长度;
(2)若该弹簧挂上一个物体后,弹簧长度为,求这个物体的质量.
经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 |
红枣 |
小米 |
规格 |
|
|
成本(元 |
40 |
38 |
售价(元 |
60 |
54 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共,其中,这种规格的红枣的销售量不低于
.假设这后五个月,销售这种规格的红枣为
,销售这种规格的红枣和小米获得的总利润为
(元
,求出
与
之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
一天,小华爸爸开车带全家到西安游玩,实现爷爷奶奶想看大雁塔,游大唐芙蓉园的愿望,由导航可知,从小华家到西安大雁塔的路程为,他们全家早上
从家出发,途中他们在一个服务区短暂休息之后,继续行驶,在上午
时,他们距离西安大雁塔还有
,如图是他们从家到西安大雁塔的过程中,行驶路程
与所用时间
之间的函数图象,请根据相关信息,解答下列问题:
(1)求小华一家在服务区休息了多长时间?
(2)求所在直线的函数表达式,并求小华一家这天几点到达西安大雁塔?

在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
品种 项目 |
产量(斤 |
销售价(元 |
成本(元 |
香瓜 |
2000 |
12 |
8000 |
甜瓜 |
4500 |
3 |
5000 |
现假设李师傅今年下半年香瓜种植的大棚数为个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为
元.
根据以上提供的信息,请你解答下列问题:
(1)求出与
之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
某樱桃种植户有20吨樱桃待售,现有两种销售方式:一是批发,二是零售.经过市场调查,这两种销售方式对这个种植户而言,每天的销量及每吨所获的利润如下表:
销售方式 |
每天销量(吨 |
每吨所获利润(元 |
批发 |
3 |
4000 |
零售 |
1 |
6000 |
假设该种植户售完20吨樱桃,共批发了吨,所获总利润为
元.
(1)求出与
之间的函数关系式;
(2)若受客观因素影响,这个种植户每天只能采用一种销售方式销售,且正好10天销售完所有樱桃,请计算该种植户所获总利润是多少元?
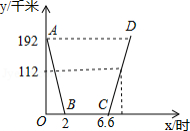
昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离 (千米)与他离家的时间 (时 之间的函数图象.
根据下面图象,回答下列问题:
(1)求线段 所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?