我省某苹果基地销售优质苹果,该基地对需要送货且购买量在 (含 和 的客户有两种销售方案(客户只能选择其中一种方案)
方案 :每千克5.8元,由基地免费送货.
方案 :每千克5元,客户需支付运费2000元.
(1)请分别写出按方案 ,方案 购买这种苹果的应付款 (元 与购买量 之间的函数表达式;
(2)求购买量 在什么范围时,选用方案 比方案 付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

相关知识点
推荐套卷
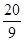 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,若篮球运行的轨迹为抛物线,篮圈中心距离地面3米.
米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,若篮球运行的轨迹为抛物线,篮圈中心距离地面3米.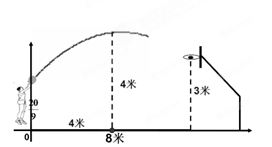

 粤公网安备 44130202000953号
粤公网安备 44130202000953号