根据记录,从地面向上以内,每升高,气温降低;又知在距离地面以上高空,气温几乎不变.若地面气温为,设距地面的高度为处的气温为
(1)写出距地面的高度在以内的与之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为时,飞机距离地面的高度为,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面时,飞机外的气温.
相关知识点
推荐套卷
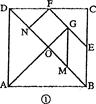


 的图象与
的图象与 轴相交于点
轴相交于点 ,顶点为
,顶点为 ,点
,点 在这个二次函数图象的对称轴上.若四边形
在这个二次函数图象的对称轴上.若四边形 是一个边长为2且有一个内角为
是一个边长为2且有一个内角为 的菱形.求此二次函数的表达式.
的菱形.求此二次函数的表达式.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号