初中数学一次函数图象上点的坐标特征填空题

如图，直线 $l$为 $y=\sqrt{3}x$，过点 $A_1(1,0)$作 $A_1{B}_1\perp x$轴，与直线 $l$交于点 $B_1$，以原点 $O$为圆心， $O{B}_1$长为半径画圆弧交 $x$轴于点 $A_2$；再作 $A_2{B}_2\perp x$轴，交直线 $l$于点 $B_2$，以原点 $O$为圆心， $O{B}_2$长为半径画圆弧交 $x$轴于点 $A_3$； $\dots \dots$，按此作法进行下去，则点 $A_n$的坐标为 $($　　 $)$．

如图，在平面直角坐标系中，点 $M$是直线 $y=-x$上的动点，过点 $M$作 $\mathit{MN}\perp x$轴，交直线 $y=x$于点 $N$，当 $\mathit{MN}⩽8$时，设点 $M$的横坐标为 $m$，则 $m$的取值范围为　            　．

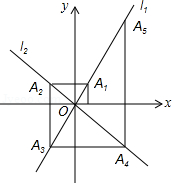
如图，在平面直角坐标系中，点 $A_1$， $A_2$， $A_3$， $\dots$和 $B_1$， $B_2$， $B_3$， $\dots$分别在直线 $y=\frac{1}{5}x+b$和 $x$轴上．△ $O{A}_1{B}_1$，△ $B_1{A}_2{B}_2$，△ $B_2{A}_3{B}_3$， $\dots$都是等腰直角三角形．如果点 $A_1(1,1)$，那么点 $A_{2018}$的纵坐标是　　．

如图，在平面直角坐标系中，直线 $l:y=\frac{\sqrt{3}}{3}x-\frac{\sqrt{3}}{3}$与 $x$轴交于点 $B_1$，以 $O{B}_1$为边长作等边三角形 $A_{1}O{B}_1$，过点 $A_1$作 $A_1{B}_2$平行于 $x$轴，交直线 $l$于点 $B_2$，以 $A_1{B}_2$为边长作等边三角形 $A_2{A}_1{B}_2$，过点 $A_2$作 $A_2{B}_3$平行于 $x$轴，交直线 $l$于点 $B_3$，以 $A_2{B}_3$为边长作等边三角形 $A_3{A}_2{B}_3$， $\dots$，则点 $A_{2017}$的横坐标是　　．

如图，点 $A_1(2,2)$在直线 $y=x$上，过点 $A_1$作 $A_1{B}_1//y$轴交直线 $y=\frac{1}{2}x$于点 $B_1$，以点 $A_1$为直角顶点， $A_1{B}_1$为直角边在 $A_1{B}_1$的右侧作等腰直角△ $A_1{B}_1{C}_1$，再过点 $C_1$作 $A_2{B}_2//y$轴，分别交直线 $y=x$和 $y=\frac{1}{2}x$于 $A_2$， $B_2$两点，以点 $A_2$为直角顶点， $A_2{B}_2$为直角边在 $A_2{B}_2$的右侧作等腰直角△ $A_2{B}_2{C}_2\dots$，按此规律进行下去，则等腰直角△ $A_n{B}_n{C}_n$的面积为　　．（用含正整数 $n$的代数式表示）

如图，在平面直角坐标系中有直线 $y=-x-1$与双曲线 $y=\frac{1}{x}$在直线上取点 $A_1$，过点 $A_1$作 $y$轴的垂线交双曲线于点 $B_1$，过 $B_1$作 $x$轴的垂线交直线于点 $A_2$，过点 $A_2$作 $y$轴的垂线交双曲线于点 $B_2$，过 $A_2$作 $x$轴的垂线交双曲线于点 $B_2$过 $B_2$作 $x$轴的垂线交直线于点 $A_3$， $\dots \dots$，按此规律继续操作下去，依次得到直线上的点 $A_1$， $A_2$， $A_3$， $\dots A_n$，记点 $A_n$的横坐标为 $a_n$，若 $a_1=-2$，则 $a_{2016}=$　　．

如图，点 $A_1(1,\sqrt{3})$在直线 $l_1:y=\sqrt{3}x$上，过点 $A_1$作 $A_1{B}_1\perp l_1$交直线 $l_2:y=\frac{\sqrt{3}}{3}x$于点 $B_1$，以 $A_1{B}_1$为边在△ $O{A}_1{B}_1$外侧作等边三角形 $A_1{B}_1{C}_1$，再过点 $C_1$作 $A_2{B}_2\perp l_1$，分别交直线 $l_1$和 $l_2$于 $A_2$， $B_2$两点，以 $A_2{B}_2$为边在△ $O{A}_2{B}_2$外侧作等边三角形 $A_2{B}_2{C}_2$， $\dots$按此规律进行下去，则第 $n$个等边三角形 $A_n{B}_n{C}_n$的面积为　　．（用含 $n$的代数式表示）

如图，点 $A_1(1,1)$在直线 $y=x$上，过点 $A_1$分别作 $y$轴、 $x$轴的平行线交直线 $y=\frac{\sqrt{3}}{2}x$于点 $B_1$， $B_2$，过点 $B_2$作 $y$轴的平行线交直线 $y=x$于点 $A_2$，过点 $A_2$作 $x$轴的平行线交直线 $y=\frac{\sqrt{3}}{2}x$于点 $B_3$， $\dots$，按照此规律进行下去，则点 $A_n$的横坐标为　　．

如图，点 $A$的坐标为 $(-4,0)$，直线 $y=\sqrt{3}x+n$与坐标轴交于点 $B$、 $C$，连接 $\mathit{AC}$，如果 $\angle \mathit{ACD}=90°$，则 $n$的值为　      　．

在平面直角坐标系中，直线 $l:y=x-1$与 $x$轴交于点 $A_1$，如图所示依次作正方形 $A_1{B}_1{C}_{1}O$、正方形 $A_2{B}_2{C}_2{C}_1$、 $\dots$、正方形 $A_n{B}_n{C}_n{C}_{n-1}$，使得点 $A_1$、 $A_2$、 $A_3$、 $\dots$在直线 $l$上，点 $C_1$、 $C_2$、 $C_3$、 $\dots$在 $y$轴正半轴上，则点 $B_n$的坐标是　          ．

如图，直线 $y=\frac{1}{2}x+1$与 $x$轴交于点 $A$，与 $y$轴交于点 $B$， $\mathit{\Delta BOC}$与△ $B\text{'}O\text{'}C\text{'}$是以点 $A$为位似中心的位似图形，且相似比为 $1:3$，则点 $B$的对应点 $B\text{'}$的坐标为　                 　．

如图，在平面直角坐标系中，直线 $l:y=x+2$交 $x$轴于点 $A$，交 $y$轴于点 $A_1$，点 $A_2$， $A_3$， $\dots$在直线 $l$上，点 $B_1$， $B_2$， $B_3$， $\dots$在 $x$轴的正半轴上，若△ $A_{1}O{B}_1$，△ $A_2{B}_1{B}_2$，△ $A_3{B}_2{B}_3$， $\dots$，依次均为等腰直角三角形，直角顶点都在 $x$轴上，则第 $n$个等腰直角三角形 $A_n{B}_{n-1}{B}_n$顶点 $B_n$的横坐标为　          　．

如图，在平面直角坐标系中，函数 $y=2x$和 $y=-x$的图象分别为直线 $l_1$， $l_2$，过点 $(1,0)$作 $x$轴的垂线交 $l_1$于点 $A_1$，过点 $A_1$作 $y$轴的垂线交 $l_2$于点 $A_2$，过点 $A_2$作 $x$轴的垂线交 $l_1$于点 $A_3$，过点 $A_3$作 $y$轴的垂线交 $l_2$于点 $A_4$， $\dots$依次进行下去，则点 $A_{2017}$的坐标为　         　．

如图，直线 $y=\frac{\sqrt{3}}{3}x$上有点 $A_1$， $A_2$， $A_3$， $\dots A_{n+1}$，且 $O{A}_1=1$， $A_1{A}_2=2$， $A_2{A}_3=4$， $A_n{A}_{n+1}=2^n$，分别过点 $A_1$， $A_2$， $A_3$， $\dots A_{n+1}$作直线 $y=\frac{\sqrt{3}}{3}x$的垂线，交 $y$轴于点 $B_1$， $B_2$， $B_3$， $\dots B_{n+1}$，依次连接 $A_1{B}_2$， $A_2{B}_3$， $A_3{B}_4$， $\dots A_n{B}_{n+1}$，得到△ $A_1{B}_1{B}_2$，△ $A_2{B}_2{B}_3$，△ $A_3{B}_3{B}_4$， $\dots$，△ $A_n{B}_n{B}_{n+1}$，则△ $A_n{B}_n{B}_{n+1}$的面积为　　．（用含正整数 $n$的式子表示）

如图，在平面直角坐标系中，直线 $l_1:y=\sqrt{3}x+\sqrt{3}$与 $x$轴交于点 $A_1$，与 $y$轴交于点 $A_2$，过点 $A_1$作 $x$轴的垂线交直线 $l_2:y=\frac{\sqrt{3}}{3}x$于点 $B_1$，过点 $A_1$作 $A_1{B}_1$的垂线交 $y$轴于点 $B_2$，此时点 $B_2$与原点 $O$重合，连接 $A_2{B}_1$交 $x$轴于点 $C_1$，得到第1个△ $C_1{B}_1{B}_2$；过点 $A_2$作 $y$轴的垂线交 $l_2$于点 $B_3$，过点 $B_3$作 $y$轴的平行线交 $l_1$于点 $A_3$，连接 $A_3{B}_2$与 $A_2{B}_3$交于点 $C_2$，得到第2个△ $C_2{B}_2{B}_3\dots \dots$按照此规律进行下去，则第2019个△ $C_{2019}{B}_{2019}{B}_{2020}$的面积是　　．