如图,在平面直角坐标系中, …,都是等边三角形,且点A1,A3,A5,A7,A9的坐标分别为 ,依据图形所反映的规律,则A100的坐标为 .

在平面直角坐标系中,点 P( x, y)经过某种变换后得到点 P'(﹣ y+1, x+2),我们把点 P'(﹣ y+1, x+2)叫做点 P( x, y)的终结点.已知点 P 1的终结点为 P 2,点 P 2的终结点为 P 3,点 P 3的终结点为 P 4,这样依次得到 P 1、 P 2、 P 3、 P 4、… P n、…,若点 P 1的坐标为(2,0),则点 P 2017的坐标为 .
如图,在平面直角坐标系中,一动点从原点 出发,沿着箭头所示方向,每次移动1个单位,依次得到点
出发,沿着箭头所示方向,每次移动1个单位,依次得到点 ,
, ,
, ,
, ,
, ,
, ,
, ,则点
,则点 的坐标是 .
的坐标是 .

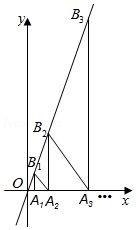
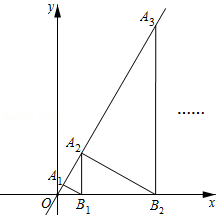
如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是 .
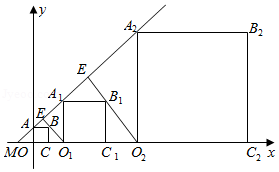
如图,过直线 上的点 作 ,交 轴于点 ,过点 作 轴.交直线 于点 ;过点 作 ,交 轴于点 ,过点 作 轴,交直线 于点 ; 按照此方法继续作下去,若 ,则线段 的长度为 .(结果用含正整数 的代数式表示)
如图,动点 从坐标原点 出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点 ,第2秒运动到点 ,第3秒运动到点 ,第4秒运动到点 则第2068秒点 所在位置的坐标是 .

如图,△,△
,△
,
,△
,都是一边在
轴上的等边三角形,点
,
,
,
,
都在反比例函数
的图象上,点
,
,
,
,
,都在
轴上,则
的坐标为 .

如图,在平面直角坐标系中,点的坐标为
,
,将线段
绕点
按顺时针方向旋转
,再将其长度伸长为
的2倍,得到线段
;又将线段
绕点
按顺时针方向旋转
,长度伸长为
的2倍,得到线段
;如此下去,得到线段
,
,
,
为正整数),则点
的坐标是 .

如图,已知直线,直线
和点
,过点
作
轴的平行线交直线
于点
,过点
作
轴的平行线交直线
于点
,过点
作
轴的平行线交直线
于点
,过点
作
轴的平行线交直线
于点
,
,按此作法进行下去,则点
的横坐标为 .

如图,在平面直角坐标系中,的顶点坐标分别为:
,
,
.已知
,作点
关于点
的对称点
,点
关于点
的对称点
,点
关于点
的对称点
,点
关于点
的对称点
,点
关于点
的对称点
,
,依此类推,则点
的坐标为 .

如图,直线的解析式为
与
轴交于点
,与
轴交于点
,以
为边作正方形
,点
坐标为
.过点
作
交
于点
,交
轴于点
,过点
作
轴的垂线交
于点
,以
为边作正方形
,点
的坐标为
.过点
作
交
于
,交
轴于点
,过点
作
轴的垂线交
于点
.以
为边作正方形
.
.则点
的坐标 .
如图,在平面直角坐标系中,四边形,
,
,
都是菱形,点
,
,
,
都在
轴上,点
,
,
,
都在直线
上,且
,
,则点
的坐标是 .

在平面直角坐标系中,抛物线的图象如图所示.已知
点坐标为
,过点
作
轴交抛物线于点
,过点
作
交抛物线于点
,过点
作
轴交抛物线于点
,过点
作
交抛物线于点
,依次进行下去,则点
的坐标为 .

如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点
,它们的半径分别为1,2,3,
,按照“加1”依次递增;一组平行线,
,
,
,
,
都与
轴垂直,相邻两直线的间距为1,其中
与
轴重合.若半径为2的圆与
在第一象限内交于点
,半径为3的圆与
在第一象限内交于点
,
,半径为
的圆与
在第一象限内交于点
,则点
的坐标为
为正整数)
