如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
已知函数 (
(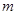 为常数).
为常数).
(1)证明:无论m取何值,该函数与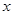 轴总有两个交点;
轴总有两个交点;
(2)设函数的两交点的横坐标分别为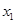 和
和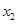 ,且
,且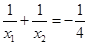 ,求此函数的解析式.
,求此函数的解析式.
已知关于 的一元二次方程
的一元二次方程 的两个实数根
的两个实数根 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
已知A=a+2,B=2a2-3a+10,C=a2+5a-3,
(1)求证:无论a为何值,A-B<0成立,并指出A,B的大小关系;
(2)请分析A与C的大小关系.
先阅读理解下面的例题,再按要求解答下列问题:
例题 :求代数式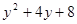 的最小值.
的最小值.
解: 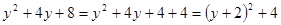
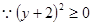

 的最小值是
的最小值是 .
.
(1)代数式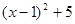 的最小值 ;
的最小值 ;
(2)求代数式 的最小值;
的最小值;
(3)某居民小区要在一块一边靠墙(墙长
 )的空地上建一个长方形花园
)的空地上建一个长方形花园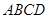 ,花园一边靠墙,另三边用总长为
,花园一边靠墙,另三边用总长为
 的栅栏围成.如图,设
的栅栏围成.如图,设 (
( ),请问:当
),请问:当 取何值时,花园的面积最大?最大面积是多少?
取何值时,花园的面积最大?最大面积是多少?
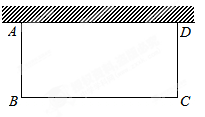
如图,利用一面墙(墙的长度为20米),用36米长的篱笆围成两个长方形鸡场,鸡场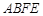 与鸡场
与鸡场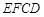 ,中间
,中间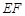 用一道篱笆隔开,每个鸡场均留一道1米宽的门,设
用一道篱笆隔开,每个鸡场均留一道1米宽的门,设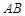 的长为
的长为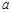
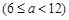 米.
米.
(1)当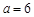 时,求点
时,求点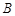 到点
到点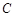 的距离;
的距离;
(2)用含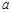 的代数式表示两个鸡场的面积和,并将所得式子化简;
的代数式表示两个鸡场的面积和,并将所得式子化简;
(3)两个鸡场的面积和有最大值吗?若有,请求出最大值;若没有,请说明理由.
(年新疆乌鲁木齐市)某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?
(年贵州省黔南州)(1)已知: ,先化简
,先化简 ,再求它的值;
,再求它的值;
(2)已知m和n是方程 的两根,求
的两根,求 .
.
已知关于x的方程x2-(m+2)x+(2m-1)=0的一个根是2,请求出方程的另一个根,并求以此两根为边长的直角三角形的面积。
已知 x1、x2是一元二次方程 的两个实数根。
的两个实数根。
(1)求 的取值范围;
的取值范围;
(2)是否存在实数 ,使
,使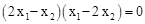 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(年湖南怀化10分)设m是不小于﹣1的实数,使得关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x 1,x2.
(1)若 ,求
,求 的值;
的值;
(2)求 的最大值.
的最大值.