专题02 代数之代数式问题(压轴题)
(2014年广西贺州3分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子 (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ,矩形的周长是2(
,矩形的周长是2( );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x= (x>0),解得x=1,这时矩形的周长2(
(x>0),解得x=1,这时矩形的周长2( )=4最小,因此
)=4最小,因此 (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子 (x>0)的最小值是( )
(x>0)的最小值是( )
| A.2 | B.1 | C.6 | D.10 |
(2014年湖南永州3分)在求1+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
S=1+6+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6,得:
6S=6+62+63+64+65+66+67+68+69+610②
②﹣①得6S﹣S=610﹣1,即5S=610﹣1,所以S= ,得出答案后,爱动脑筋的小林想:
,得出答案后,爱动脑筋的小林想:
如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是( )
A. |
B. |
C. |
D. |
(2014年新疆乌鲁木齐4分)已知m,n,k为非负实数,且m﹣k+1=2k+n=1,则代数式2k2﹣8k+6的最小值为( )
A.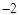 |
B. |
C.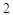 |
D.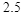 |
(2014年江苏镇江2分)读取表格中的信息,解决问题.
| n=1 |
 |
 |
 |
| n=2 |
a2=b1+2c1 |
b2=c1+2a1 |
c2=a1+2b1 |
| n=3 |
a3=b2+2c2 |
b3=c2+2a2 |
c=a2+2b2 |
| … |
… |
… |
… |
满足 的n可以取得的最小整数是 .
的n可以取得的最小整数是 .
(2014年山东菏泽3分)下面是一个按某种规律排列的数阵:

根据数阵排列的规律,第n(n是整数,且n>3)行从左向右数第 个数是 . (用含n的代数式表示)
个数是 . (用含n的代数式表示)
(2014年四川巴中3分)如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 (n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,
(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如, 展开式中的系数1、2、1恰好对应图中第三行的数字;再如,
展开式中的系数1、2、1恰好对应图中第三行的数字;再如, 展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出
展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出 的展开式为 .
的展开式为 .
(2014年浙江台州5分)有一个计算程序,每次运算都是把一个数先乘以2,再乘以它与1的和,多次重复进行这种运算的过程如下∶

则第n次的运算结果= (含字母x和n的代数式表示).
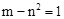 ,则代数式
,则代数式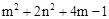 的最小值等于 .
的最小值等于 . 是从
是从 这三个数中取值的一列数,若
这三个数中取值的一列数,若 ,
, ,则
,则 中为0的个数 .
中为0的个数 . 的两实数根为x1,x2,且x12+x22=3,则m= .
的两实数根为x1,x2,且x12+x22=3,则m= . ;
; ;
; ;
; ;
; = .(用含n的代数式表示,n是正整数,且n≥2)
= .(用含n的代数式表示,n是正整数,且n≥2) ,求
,求 的值;
的值; 的最大值.
的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号