列方程解应用题
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮的传播就会有144台电脑被感染,请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
已知关于的一元二次方程
.
(1)求证:对于任意实数,方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为,
,当
时,求
的值.
有一电脑程序:每按一次按键,屏幕的 区就会自动加上 ,同时 区就会自动减去 ,且均显示化简后的结果.已知 , 两区初始显示的分别是25和 ,如图.
如,第一次按键后, , 两区分别显示:
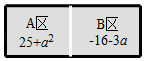
(1)从初始状态按2次后,分别求 , 两区显示的结果;
(2)从初始状态按4次后,计算 , 两区代数式的和,请判断这个和能为负数吗?说明理由.

关于的一元二次方程
.
(1)当时,利用根的判别式判断方程根的情况;
(2)若方程有两个相等的实数根,写出一组满足条件的,
的值,并求此时方程的根.
关于的一元二次方程
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求的取值范围.
阅读下列材料:
北京市正围绕着"政治中心、文化中心、国际交往中心、科技创新中心"的定位,深入实施"人文北京、科技北京、绿色北京"的发展战略."十二五"期间,北京市文化创意产业展现了良好的发展基础和巨大的发展潜力,已经成为首都经济增长的支柱产业.
2011年,北京市文化创意产业实现增加值1938.6亿元,占地区生产总值的 .2012年,北京市文化创意产业继续呈现平稳发展态势,实现产业增加值2189.2亿元,占地区生产总值的 ,是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年,北京市文化产业实现增加值2406.7亿元,比上年增长 ,文化创意产业作为北京市支柱产业已经排到了第二位.2014年,北京市文化创意产业实现增加值2794.3亿元,占地区生产总值的 ,创历史新高,2015年,北京市文化创意产业发展总体平稳,实现产业增加值3072.3亿元,占地区生产总值的 .
根据以上材料解答下列问题:
(1)用折线图将 年北京市文化创意产业实现增加值表示出来,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2016年北京市文化创意产业实现增加值约 ,亿元,你的预估理由 .
关于 的一元二次方程 有两个不相等的实数根.
(1)求 的取值范围;
(2)写出一个满足条件的 的值,并求此时方程的根.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2=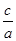 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=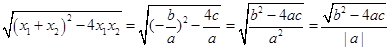 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.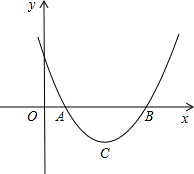
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
阅读材料:用配方法求最值.已知x,y为非负实数,
∵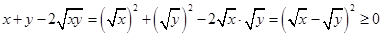
∴ ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求 的最小值.
的最小值.
解: ,当
,当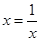 ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求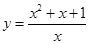 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
列方程解应用题:
随着人们节能意识的增强,节能产品的销售量逐年增加.某地区高效节能灯的年销售量2009年为10万只,预计2011年将达到14.4万只.求该地区2009年到2011年高效节能灯年销售量的平均增长率.
请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程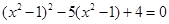 ,我们可以将
,我们可以将 视为一个整体,然后设
视为一个整体,然后设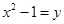 ,则原方程可化为
,则原方程可化为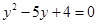 ①
①
解得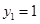 ,
,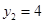 ,当y=1时,
,当y=1时,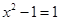 ,∴
,∴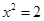 ,
, ;
;
当y=4时,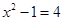 ,∴
,∴ ,
,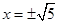 ,∴原方程的解为
,∴原方程的解为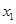 =
=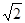 ,
,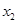 =-
=-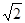 ,
,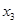 =
=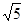 ,
,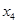 =-
=-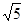 .
.
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_________法达到了降次的目的,体现了_________的数学思想.
(2)解方程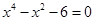 .
.
某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R、P与x的关系式分别为R=500+30x,P=170-2x.
(1)当日产量为多少时,,?
(2)当日产量为多少时,可获得最大利润?最大利润是多少?