如图,从边长为 的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠无缝隙),则拼成的长方形的另一边长是 .

如图所示,图1是一个边长为 的正方形剪去一个边长为1的小正方形,图2是一个边长为 的正方形,记图1,图2中阴影部分的面积分别为 , ,则 可化简为 .

如图,将边长为 的正方形纸板沿虚线剪成两个小正方形和两个矩形,拿掉边长为 的小正方形纸板后,将剩下的三块拼成新的矩形.
(1)用含 或 的代数式表示拼成矩形的周长;
(2) , ,求拼成矩形的面积.

如图1,将边长为 的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在矩形 中, 为 中点,以 为边作正方形 ,边 交 于点 ,在边 上取点 使 ,作 交 于点 ,交 于点 ,欧几里得在《几何原本》中利用该图解释了 ,现以点 为圆心, 为半径作圆弧交线段 于点 ,连结 ,记 的面积为 ,图中阴影部分的面积为 .若点 , , 在同一直线上,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形ABCD与四边形BEFG都是正方形,设AB=a,DE=b(a>b).
(1)写出AG的长度(用含字母a、b的代数式表示);
(2)观察图形,试用不同的方法表示图形中阴影部分的面积,你能获得相应的一个因式分解公式吗?请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2.试利用⑵中的公式,求a、b的值.
如图,边长为(
 )的正方形纸片剪出一个边长为
)的正方形纸片剪出一个边长为 的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为4,则另一边长是_____________.
的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为4,则另一边长是_____________.
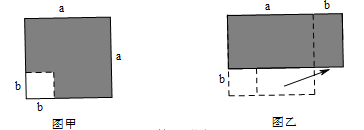
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),由两个图形中阴影部分的面积相等,可以验证 (填写序号).
①
②
③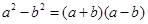
④
如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的公式是 ( )

| A.a2+b2=(a+b)(a-b) |
| B.a2-b2=(a+b)(a-b) |
| C.(a+b)2=a2+2ab+b2 |
| D.(a-b)2=a2-2ab+b2 |