初中数学幂的乘方与积的乘方解答题

运动会前夕，为了提高体能，小明每天放学回家做仰卧起坐．他制作   
了一张表格记录自己每天做仰卧起坐的成绩．以每分钟做40个为标准，超过的个数记为正，不足的个数记为负．下表是小明一周做仰卧起坐的记录：

时间	星期一	星期二	星期三	星期四	星期五	星期六	星期日
个数	+14	+8	-5	+2	-10	+1	-3

 
根据上述记录表，回答下列问题：
（1）小明这周一天最多做       个，最少做       个；
（2）这周小明平均每天做多少个？

一只蜗牛从A点出发，在一条数轴上来回爬行，规定：向正半轴运动记为“+”，向负半轴运动记为“—”，从开始到结束爬行的各段路程（单位：cm）依次为+7，—5，
—10，—8，+9，—6，+12，+4。
（1）若A点在数轴上表示的数为—2，则蜗牛停在数轴上何处，请通过计算加以说明。
（2）若蜗牛的爬行速度为每秒，请问蜗牛一共爬行了多少秒？

在+3，0，，，，这六个数中，负数有m个，整数有n个，非负数有k个，求的值。

某食品厂从生产的袋装食品中随机抽样检测20袋的质量是否符合标准质量，超过或不足的质量分别用正、负数表示，例如＋2表示该袋食品超过标准质量2g，现记录如下：

与标准质量的误差（g）	－5	－2	0	+1	+3	+6
袋数	5	3	3	4	2	3

（1）在抽取的样品中，最重的那袋食品的质量比最轻的那袋多了多少克？
（2）若标准质量为100g／袋，则这次抽样检测的总质量是多少克？

（1）在数1．2．3．4．5．6．7．8前添加“+”，“-”并依次运算，所得结果可能的最小非负数是多少？（列式计算，列出一个算式即可）
（2）在数1．2．3……2015前添加“+”，“-”并依次运算，所得结果可能的最小非负数是多少？
（列式计算，列出一个算式即可）
（3）在数1．2．3……n前添加“+”，“-”并依次运算，所得结果可能的最小非负数是多少？（只写出答案即可）

有20筐白菜，以每筐25千克为标准，超过或不足的分别用正、负来表示，记录如下：

与标准质量的差（单位：千克）	－3	－2	－1.5	0	1	2.5
筐数	1	4	2	3	2	8

 
（1）与标准质量比较，20筐白菜总计超过或不足多少千克？
（2）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？

把下列各数在数轴上表示出来，并用“＜”号连接．
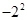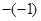，  ，  0，   -|-2︳， 2．5       |-3︳

已知A、B在数轴上分别表示m、n填写下表

m	5	－5	－6	－6	－10	－2．5
n	3	0	4	－4	2	－2．5
A、B两点间距离

（2）若A、B两点间距离为d，则d与m，n有何数量关系？

一小虫从某点O出发在一天直线上来回爬行，假定向右爬行的路程记为正数，向左爬行的路程记为负数，爬过的各段路程依次为：（单位：厘米） +2，-6，-6，+12，-10，+11，-3
（1）小虫最后是否回到出发点O呢？ 
小虫离开出发点O最远是多少厘米？
在爬行过程中，如果每爬行1厘米奖励三支铅笔，那么小虫一共得到了多少支铅笔呢？

（本题6分）有理数a，b，c在数轴上的位置如图所示，

（1）c__________0； b+c__________0；b－a__________0（用“＞、＜、=”填空）
（2）试化简：|b－a |－| b+c |+|c|．

（本题8分）某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：

（1）根据记录的数据可知该厂这周星期四生产自行车_______辆；
（2）这周产量最多的一天比产量最少的一天多生产自行车_______辆；
（3）根据记录的数据可知该厂本周实际生产自行车_______辆；
（4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另外奖励20元，少生产一辆扣25元，那么该厂工人这一周的工资总额是多少元？

超市9月1日到5日的收入、支出情况如下表

日期	1日	2日	3日	4日	5日
支出（元）	150	260	180	130	210
收入（元）	160	240	150	180	300

 
运用你学的知识，给商店简单的记一笔帐．
（1）哪几天是亏本，那几天是盈利的？
（2）9月1日到5日，该超市总支出是多少？

如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2011个格子中的数为 （     ）．

A．3

B．2

C．0

D．－1

已知a、b互为相反数，c、d互为倒数，m的绝对值是2，求的值．

观察下列有规律的数：，，，，，……根据规律可知，
（1）第7个数_____________,第n个数是______________（n是正整数）．
（2） 是第__________个数．
（3）计算．（本题6分）