有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4可作运算:(1+2+3)×4=24.[注意上述运算与4×(2+3+1)应视为相同方法的运算].现有四个有理数3,4,﹣6,10,运用上述规则写出三种不同方法的运算式,使其结果等于24,运算式如下:
(1) ;
(2) ;
(3) .
初一年级举行篮球循环赛,规则是:胜一场得2分,平一场得0分,负一场得﹣2分,比赛结果是初一(3)班2胜1平4负,问该班最后得分是多少?
已知2a=m,32b=n,a,b为正整数,求23a+10b的值.
观察下列计算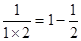 ,
,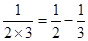 ,
, ,
,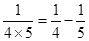 ……
……
(1)第5个式子是 ;第n个式是 。
(2)从计算结果中找规律,利用规律计算
(3)计算
某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| -3 |
+7 |
-9 |
+8 |
+6 |
-5 |
-4 |
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了 层.将图1倒置后与原图拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层.将图1倒置后与原图拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为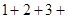 …
…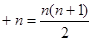 .
.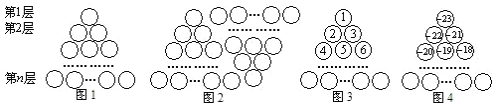
如果图1中的圆圈共有12层,
(1)当有12层时,图中共有 个圆圈;
(2)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数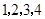 ,…,则最底层最左边这个圆圈中的数是 ;
,…,则最底层最左边这个圆圈中的数是 ;
(3)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数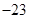 ,
,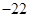 ,
, ,…,求图4中所有圆圈中各数之和.
,…,求图4中所有圆圈中各数之和.
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放十六粒……按这个方法放满整个棋盘就行。”国王以为要不了多少粮食,就随口答应了,结果国王输了.
(1)我们知道,国际象棋共有64个格子,则在第64格中应放多少米?(用幂表示)
(2)请探究第(1)中的数的末位数字是多少?(简要写出探究过程.)
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
用分数表示无限循环小数: .
.
解:设 ①.等式两边同时乘以10,得
①.等式两边同时乘以10,得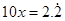 ②.
②.
将②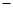 ①得:
①得: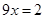 ,则
,则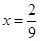 ,∴
,∴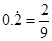 .
.
请参照以上解法求出国王输给阿基米德的米粒数(用幂的形式表示).
观察下列等式:
第1个等式:a1=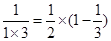 ;
;
第2个等式:a2= ;
;
第3个等式:a3=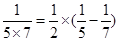 ;
;
第4个等式:a4=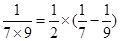
 =
=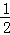 ×(
×(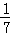 -
-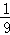 );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
某班抽查了10名同学的期末成绩,以80分为基准,超出的记为正数,不足的记为负数,记录的结果如下:
+8,-3,+12,-7,-10,-3,-8,+1,0,+10.
(1)这10名同学中最高分是多少?最低分是多少?
(2)10名同学中,低于80分的所占的百分比是多少?
(3)10名同学的平均成绩是多少?
有20筐白菜,以每筐25千克为标准,超过或不足的分别用正、负来表示,记录如下:
| 与标准质量的差(单位:千克) |
-3 |
-2 |
-1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
(1)与标准质量比较,20筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?