一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“—”,从开始到结束爬行的各段路程(单位:cm)依次为+7,—5,
—10,—8,+9,—6,+12,+4。
(1)若A点在数轴上表示的数为—2,则蜗牛停在数轴上何处,请通过计算加以说明。
(2)若蜗牛的爬行速度为每秒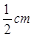 ,请问蜗牛一共爬行了多少秒?
,请问蜗牛一共爬行了多少秒?
相关知识点
推荐套卷
一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“—”,从开始到结束爬行的各段路程(单位:cm)依次为+7,—5,
—10,—8,+9,—6,+12,+4。
(1)若A点在数轴上表示的数为—2,则蜗牛停在数轴上何处,请通过计算加以说明。
(2)若蜗牛的爬行速度为每秒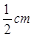 ,请问蜗牛一共爬行了多少秒?
,请问蜗牛一共爬行了多少秒?