观察下面由正整数组成的数阵:
照此规律,按从上到下、从左到右的顺序,第50行的第50个数是()
| A.2450 | B.2451 | C.2550 | D.2551 |
将正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是()
| A.502 | B.503 | C.504 | D.505 |
下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为()
| A.135 | B.170 | C.209 | D.252 |
如图,是一组按照某种规律摆放而成的图案,第1个图有1个三角形,第二个图有4个三角形,第三个图有8个三角形,第四个图有12个三角形,则图5中三角形的个数是()
| A.8 | B.12 | C.16 | D.17 |
下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是()
| A.495 | B.497 | C.501 | D.503 |
记 ,令
,令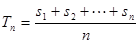 ,则称
,则称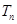 为
为 ,
, ,……,
,……, 这列数的“凯森和”.已知
这列数的“凯森和”.已知 ,
, ,……,
,……,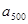 的“凯森和”为2004,那么13,
的“凯森和”为2004,那么13, ,
, ,……,
,……,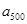 的“凯森和”为()
的“凯森和”为()
| A.2013 | B.2015 | C.2017 | D.2019 |
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()
| A.36=15+21 | B.49=18+31 | C.25="9+16" | D.13=3+10 |
定义一种运算: ,其中k是正整数,且k ≥2,[x]表示非
,其中k是正整数,且k ≥2,[x]表示非
负实数x的整数部分,例如[2.6]=2,[0.8]=0.若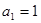 ,则
,则 的值为()
的值为()
| A.2015 | B.4 | C.2014 | D.5 |
如图,是一组按照某种规律摆放而成的图案,第1个图有1个三角形,第二个图有4个三角形,第三个图有8个三角形,第四个图有12个三角形,则图5中三角形的个数是()
| A.8 | B.12 | C.16 | D.17 |
如图,数轴上的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a-c|之值与下列选项中哪个不同()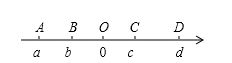
A.|a-b|+|c-b| B.|a|+|d|-|c+d|
C.|a-d|-|d-c| D.|a|+|d|-|c-d|
如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第 个图形需要黑色棋子的个数是.
个图形需要黑色棋子的个数是.
如图,是一组按照某种规律摆放成的图案,则图6中三角形的个数是()
| A.18 | B.19 | C.20 | D.21 |
亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会,并在会上投票选出2022年第19届亚运会举办城市为杭州.5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2015年9月16日20时应是()
| A.伦敦时间2015年9月16日11时 |
| B.巴黎时间2015年9月16日13时 |
| C.智利时间2015年9月16日5时 |
| D.曼谷时间2015年9月16日18时 |
如图所示的数码叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为 ,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为()
,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为()
A. |
B. |
C. |
D. |