初中数学规律型：数字的变化类试题

观察下列各式：

$\frac{2}{1\times 3}=\frac{1}{1}-\frac{1}{3}$；

$\frac{2}{2\times 4}=\frac{1}{2}-\frac{1}{4}$；

$\frac{2}{3\times 5}=\frac{1}{3}-\frac{1}{5}$；

$\dots$

请利用你所得结论，化简代数式： $\frac{1}{1\times 3}+\frac{1}{2\times 4}+\frac{1}{3\times 5}+\dots +\frac{1}{n(n+2)}(n⩾3$且 $n$为整数），其结果为　　．

如表被称为“杨辉三角”或“贾宪三角”．其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和．表中两平行线之间的一列数：1，3，6，10，15， $\dots$，我们把第一个数记为 $a_1$，第二个数记为 $a_2$，第三个数记为 $a_3$， $\dots$，第 $n$个数记为 $a_n$，则 $a_4+a_{200}=$　 　．

一列数 $a_1$， $a_2$， $a_3$， $\dots$满足条件： $a_1=\frac{1}{2}$， $a_n=\frac{1}{1-a_{n-1}}(n⩾2$，且 $n$为整数），则 $a_{2016}=$　        　．

我国古代数学家杨辉发现了如图所示的三角形，我们称之为“杨辉三角”从图中取一列数：1，3，6，10， $\dots$，记 $a_1=1$， $a_2=3$， $a_3=6$， $a_4=10$， $\dots$，那么 $a_9+a_{11}-2a_{10}+10$的值是　       　．

在求 $1+3+3^2+3^3+3^4+3^5+3^6+3^7+3^8$的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设： $S=1+3+3^2+3^3+3^4+3^5+3^6+3^7+3^8$①，

然后在①式的两边都乘以3，得： $3S=3+3^2+3^3+3^4+3^5+3^6+3^7+3^8+3^9$②，

② $-$①得， $3S-S=3^9-1$，即 $2S=3^9-1$，

所以 $S=\frac{3^9-1}{2}$．

得出答案后，爱动脑筋的张红想：如果把“3”换成字母 $m(m\ne 0$且 $m\ne 1)$，能否求出 $1+m+m^2+m^3+m^4+\dots +m^{2016}$的值？如能求出，其正确答案是　                              　．

在一列数： $a_1$， $a_2$， $a_3$， $\dots$， $a_n$中， $a_1=3$， $a_2=7$，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这一列数中的第2017个数是 $($　　 $)$

A．1B．3C．7D．9

将正整数1至2018按一定规律排列如下表：

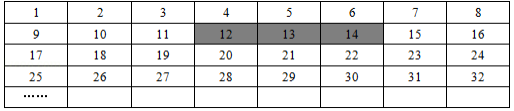
平移表中带阴影的方框，方框中三个数的和可能是 $($　　 $)$

A．2019B．2018C．2016D．2013

按一定规律排成的一列数依次为： $\frac{1}{2}$， $\frac{\sqrt{2}}{3}$， $\frac{\sqrt{3}}{10}$， $\frac{2}{15}$， $\frac{\sqrt{5}}{26}$， $\frac{\sqrt{6}}{35}$， $\dots$按此规律排下去，这列数中的第10个数是　　．

定义一种对正整数 $n$的“ $F$”运算：①当 $n$为奇数时， $F\left(n\right)=3n+1$；②当 $n$为偶数时， $F\left(n\right)=\frac{n}{2^k}$（其中 $k$是使 $F\left(n\right)$为奇数的正整数） $\dots \dots$，两种运算交替重复进行，例如，取 $n=24$，则：

若 $n=13$，则第2018次“ $F$”运算的结果是 $($　　 $)$

A．1B．4C．2018D． $4^{2018}$

根据下列材料，解答问题．

等比数列求和：

概念：对于一列数 $a_1$， $a_2$， $a_3$， $\dots a_n\dots (n$为正整数），若从第二个数开始，每一个数与前一个数的比为一定值，即 $\frac{a_k}{a_{k-1}}=q$（常数），那么这一列数 $a_1$， $a_2$， $a_3$， $\dots$， $a_n$， $\dots$成等比数列，这一常数 $q$叫做该数列的公比．

例：求等比数列1，3， $3^2$， $3^3$， $\dots$， $3^{100}$的和，

解：令 $S=1+3+3^2+3^3+\dots +3^{100}$

则 $3S=3+3^2+3^3+\dots +3^{100}+3^{101}$

因此， $3S-S=3^{101}-1$，所以 $S=\frac{3^{101}-1}{2}$

即 $1+3+3^2+3^3\dots +3^{100}=\frac{3^{101}-1}{2}$

仿照例题，等比数列1，5， $5^2$， $5^3$， $\dots$， $5^{2018}$的和为　　．

设 $a_1$， $a_2$， $a_3\dots \dots$是一列正整数，其中 $a_1$表示第一个数， $a_2$表示第二个数，依此类推， $a_n$表示第 $n$个数 $(n$是正整数）．已知 $a_1=1$， $4a_n={(a_{n+1}-1)}^2-{(a_n-1)}^2$，则 $a_{2018}=$　　．

对于任意大于0的实数 $x$、 $y$，满足： ${\log }_2(x·y)={\log }_{2}x+{\log }_{2}y$，若 ${\log }_{2}2=1$，则 ${\log }_{2}16=$　　．

观察以下等式：

第1个等式： $\frac{1}{3}\times (1+\frac{2}{1})=2-\frac{1}{1}$，

第2个等式： $\frac{3}{4}\times (1+\frac{2}{2})=2-\frac{1}{2}$，

第3个等式： $\frac{5}{5}\times (1+\frac{2}{3})=2-\frac{1}{3}$，

第4个等式： $\frac{7}{6}\times (1+\frac{2}{4})=2-\frac{1}{4}$．

第5个等式： $\frac{9}{7}\times (1+\frac{2}{5})=2-\frac{1}{5}$．

$\dots$

按照以上规律，解决下列问题：

（1）写出第6个等式：　 $\frac{11}{8}\times (1+\frac{2}{6})=2-\frac{1}{6}$　；

（2）写出你猜想的第 $n$个等式：　　（用含 $n$的等式表示），并证明．

生活中常用的十进制是用 $0~9$ 这十个数字来表示数，满十进一，例： $12=1\times 10+2$ ， $212=2\times 10\times 10+1\times 10+2$ ；计算机也常用十六进制来表示字符代码，它是用 $0~F$ 来表示 $0~15$ ，满十六进一，它与十进制对应的数如表：

十进制	0	1	2	$\dots$	8	9	10	11	12	13	14	15	16	17	$\dots$
十六进制	0	1	2	$\dots$	8	9	$A$	$B$	$C$	$D$	$E$	$F$	10	11	$\dots$

例：十六进制 $2B$ 对应十进制的数为 $2\times 16+11=43$ ， $10C$ 对应十进制的数为 $1\times 16\times 16+0\times 16+12=268$ ，那么十六进制中 $14E$ 对应十进制的数为 $($ 　　 $)$

A．

28

B．

62

C．

238

D．

334

将从1开始的自然数按以下规律排列，例如位于第3行、第4列的数是12，则位于第45行、第8列的数是　　．