初中数学规律型：数字的变化类试题

将正整数1至2018按一定规律排列如下表：

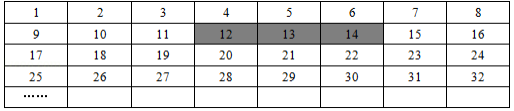
平移表中带阴影的方框，方框中三个数的和可能是 $($　　 $)$

A．2019B．2018C．2016D．2013

观察以下等式：

第1个等式： $\frac{1}{3}\times (1+\frac{2}{1})=2-\frac{1}{1}$，

第2个等式： $\frac{3}{4}\times (1+\frac{2}{2})=2-\frac{1}{2}$，

第3个等式： $\frac{5}{5}\times (1+\frac{2}{3})=2-\frac{1}{3}$，

第4个等式： $\frac{7}{6}\times (1+\frac{2}{4})=2-\frac{1}{4}$．

第5个等式： $\frac{9}{7}\times (1+\frac{2}{5})=2-\frac{1}{5}$．

$\dots$

按照以上规律，解决下列问题：

（1）写出第6个等式：　 $\frac{11}{8}\times (1+\frac{2}{6})=2-\frac{1}{6}$　；

（2）写出你猜想的第 $n$个等式：　　（用含 $n$的等式表示），并证明．

古希腊数学家把1、3、6、10、15、21、 $\dots$叫做三角形数，其中1是第一个三角形数，3是第二个三角形数，6是第三个三角形数， $\dots$，依此类推，第100个三角形数是　　．

按规律排列的一组数据： $\frac{1}{2}$ ， $\frac{3}{5}$ ，□， $\frac{7}{17}$ ， $\frac{9}{26}$ ， $\frac{11}{37}$ ， $\dots$ ，其中□内应填的数是 $($ 　　 $)$

A．

$\frac{2}{3}$

B．

$\frac{5}{11}$

C．

$\frac{5}{9}$

D．

$\frac{1}{2}$

如图所示，是一个运算程序示意图．若第一次输入 $k$的值为125，则第2018次输出的结果是　      　．

按一定规律排列的单项式： $a$， $-2a$， $4a$， $-8a$， $16a$， $-32a$， $\dots$，第 $n$个单项式是 $($　　 $)$

A． ${(-2)}^{n-1}a$B． ${(-2)}^{n}a$C． $2^{n-1}a$D． $2^{n}a$

小光和小王玩“石头、剪子、布”游戏，规定：一局比赛后，胜者得3分，负者得 $-1$分，平局两人都得0分，小光和小王都制订了自己的游戏策略，并且两人都不知道对方的策略．

小光的策略是：石头、剪子、布、石头、剪子、布、 $\dots \dots$

小王的策略是：剪子、随机、剪子、随机 $\dots \dots$（说明：随机指石头、剪子、布中任意一个）

例如，某次游戏的前9局比赛中，两人当时的策略和得分情况如下表

局数	1	2	3	4	5	6	7	8	9
小光实际策略	石头	剪子	布	石头	剪子	布	石头	剪子	布
小王实际策略	剪子	布	剪子	石头	剪子	剪子	剪子	石头	剪子
小光得分	3	3	$-1$	0	0	$-1$	3	$-1$	$-1$
小王得分	$-1$	$-1$	3	0	0	3	$-1$	3	3

已知在另一次游戏中，50局比赛后，小光总得分为 $-6$分，则小王总得分为　     　分．

将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是 $($ 　　 $)$

A．

2025

B．

2023

C．

2021

D．

2019

按一定规律排列的单项式： $a^2$ ， $4a^3$ ， $9a^4$ ， $16a^5$ ， $25a^6$ ， $\dots$ ，第 $n$ 个单项式是 $($ 　　 $)$

A．

$n^2{a}^{n+l}$

B．

$n^2{a}^{n-1}$

C．

$n^n{a}^{n+1}$

D．

${(n+1)}^2{a}^n$

观察下列等式： $1=1^2-0^2$， $3=2^2-1^2$， $5=3^2-2^2$， $\dots$按此规律，则第 $n$个等式为 $2n-1=$　　．

填在下面各正方形中四个数之间都有相同的规律，根据这种规律 $m$的值为 $($　　 $)$

A．180B．182C．184D．186

如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确定 $x$的值为　      　．

如图，在 $6\times 6$的网格内填入1至6的数字后，使每行、每列、每个小粗线框中的数字不重复，则 $a\times c=$　   　．

观察下列等式：

$\frac{1}{1\times 2}=1-\frac{1}{2}=\frac{1}{2}$

$\frac{1}{1\times 2}+\frac{1}{2\times 3}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}=\frac{2}{3}$

$\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}=\frac{3}{4}$

$\dots$

请按上述规律，写出第 $n$个式子的计算结果 $(n$为正整数）　   　．（写出最简计算结果即可）

观察下列等式：

第一个等式：

第二个等式：

第三个等式：

第四个等式：

按上述规律，回答下列问题：

（1）请写出第六个等式：　　　　；

（2）用含的代数式表示第个等式：　　　　；

（3）　　（得出最简结果）；

（4）计算：．