初中数学规律型：数字的变化类试题

如图，正方形 $\mathit{ABCD}$的边长为2，其面积标记为 $S_1$，以 $\mathit{CD}$为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为 $S_2$， $\dots$，按照此规律继续下去，则 $S_9$的值为 $($　　 $)$

A． ${\left(\frac{1}{2}\right)}^6$B． ${\left(\frac{1}{2}\right)}^7$C． ${\left(\frac{\sqrt{2}}{2}\right)}^6$D． ${\left(\frac{\sqrt{2}}{2}\right)}^7$

按一定规律排列的一列数依次为： $-\frac{a^2}{2}$， $\frac{a^5}{5}$， $-\frac{a^8}{10}$， $\frac{a^{11}}{17}$， $\dots (a\ne 0)$，按此规律排列下去，这列数中的第 $n$个数是　　． $(n$为正整数）

将全体正奇数排成一个三角形数阵：

1

3 5

7     9     11

13   15    17    19

21    23    25   27   29

$\dots$

按照以上排列的规律，第25行第20个数是 $($　　 $)$

A．639B．637C．635D．633

将从1开始的连续自然数按图规律排列：规定位于第 $m$行，第 $n$列的自然数10记为 $(3,2)$，自然数15记为 $(4,2)\dots$按此规律，自然数2018记为　　

列 行	第1列	第2列	第3列	第4列
第1行	1	2	3	4
第2行	8	7	6	5
第3行	9	10	11	12
第4行	16	15	14	13
$\dots$	$\dots$	$\dots$	$\dots$	$\dots$
第 $n$行	$\dots$	$\dots$	$\dots$	$\dots$

填在下面各正方形中四个数之间都有相同的规律，根据这种规律 $m$的值为 $($　　 $)$

A．180B．182C．184D．186

有2019个数排成一行，对于任意相邻的三个数，都有中间的数等于前后两数的和．如果第一个数是0，第二个数是1，那么前6个数的和是 　         　，这2019个数的和是 　          　．

观察下列各式的规律：

$(x-1)(x+1)=x^2-1$

$(x-1)(x^2+x+1)=x^3-1$

$(x-1)(x^3+x^2+x+1)=x^4-1$

$\dots$

可得到 $(x-1)(x^7+x^6+x^5+x^4+x^3+x^2+x+1)=$　         　；

一般地 $(x-1)(x^n+x^{n-1}+x^5+\dots +x^2+x+1)=$　             　．

已知 $a>0$， $S_1=\frac{1}{a}$， $S_2=-S_1-1$， $S_3=\frac{1}{S_2}$， $S_4=-S_3-1$， $S_5=\frac{1}{S_4}$， $\dots$（即当 $n$为大于1的奇数时， $S_n=\frac{1}{S_{n-1}}$；当 $n$为大于1的偶数时， $S_n=-S_{n-1}-1)$，按此规律， $S_{2018}=$　　．

如图，下列各图形中的三个数之间均具有相同的规律，依此规律，那么第4个图形中的 $x=$　      　，一般地，用含有 $m$， $n$的代数式表示 $y$，即 $y=$　    　．

观察下列等式： $1=1^2-0^2$， $3=2^2-1^2$， $5=3^2-2^2$， $\dots$按此规律，则第 $n$个等式为 $2n-1=$　　．

我国南宋数学家杨辉所著的《详解九章算术》一书中，用如图的三角形解释二项式 ${(a+b)}^n$的展开式的各项系数，此三角形称为“杨辉三角”

根据”杨辉三角”请计算 ${(a+b)}^8$的展开式中从左起第四项的系数为 $($　　 $)$

A．84B．56C．35D．28

定义一种对正整数 $n$的“ $F$”运算：①当 $n$为奇数时， $F\left(n\right)=3n+1$；②当 $n$为偶数时， $F\left(n\right)=\frac{n}{2^k}$（其中 $k$是使 $F\left(n\right)$为奇数的正整数） $\dots \dots$，两种运算交替重复进行，例如，取 $n=24$，则：

若 $n=13$，则第2018次“ $F$”运算的结果是 $($　　 $)$

A．1B．4C．2018D． $4^{2018}$

观察“田”字中各数之间的关系：

则 $c$的值为　　．

观察下列等式：

第一个等式：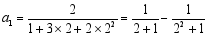

第二个等式：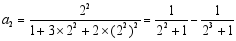

第三个等式：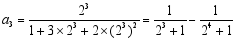

第四个等式：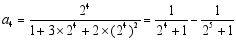

按上述规律，回答下列问题：

（1）请写出第六个等式：　　　　；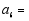

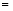（2）用含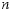的代数式表示第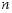个等式：　　　　；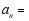

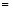（3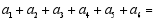）　　（得出最简结果）；

（4）计算：．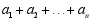

生活中常用的十进制是用 $0~9$ 这十个数字来表示数，满十进一，例： $12=1\times 10+2$ ， $212=2\times 10\times 10+1\times 10+2$ ；计算机也常用十六进制来表示字符代码，它是用 $0~F$ 来表示 $0~15$ ，满十六进一，它与十进制对应的数如表：

十进制	0	1	2	$\dots$	8	9	10	11	12	13	14	15	16	17	$\dots$
十六进制	0	1	2	$\dots$	8	9	$A$	$B$	$C$	$D$	$E$	$F$	10	11	$\dots$

例：十六进制 $2B$ 对应十进制的数为 $2\times 16+11=43$ ， $10C$ 对应十进制的数为 $1\times 16\times 16+0\times 16+12=268$ ，那么十六进制中 $14E$ 对应十进制的数为 $($ 　　 $)$

A．

28

B．

62

C．

238

D．

334