下面是小明同学做过的两道题，请先阅读解题过程，然后回答所提出的问题．
（1）计算：（1）
；
解：原式＝
第①步
＝12 第②步
问题：上述解法中，第几步有错？______（填序号即可）．
本题的正确解法是：____________
（2）
．
解：原式=
第①步
=
第②步
第③步
第④步
问题：上述解法中，第几步有错？______（填序号即可）．
本题的正确解法是：____________
2015年9月24日台风杜鹃登陆，给我福建、浙江等地造成严重影响．为民排忧解难的解放军叔叔驾着冲锋舟沿一条东西方向的河流营救灾民，早晨从A地出发，晚上最后到达B地，约定向东为正方向，当天航行依次记录如下（单位：千米）：
14，﹣9，18，﹣7，13，﹣6，10，﹣5
问：（1）B地在A地的东面，还是西面？与A地相距多少千米？
（2）这一天冲锋舟离A地最远多少千米？
（3）若冲锋舟每千米耗油0．5升，油箱容量为30升，求途中至少需要补充多少升油？
一辆公共汽车从起点站开出后，途中经过6个停靠站，最后到达终点站。下表记录了这辆公共汽车全程载客变化情况。
| 停靠站 |
起点站 |
中间 第1站 |
中间 第2站 |
中间 第3站 |
中间 第4站 |
中间 第5站 |
中间 第6站 |
终点站 |
| 上下车人数 |
+21 |
-3 +8 |
-4 +2 |
0 +4 |
-7 +1 |
-9 +6 |
-7 0 |
-12 |
（1）中间第4站上车人数是人_________，下车人数是人_________；
（2）中间的6个站中，第_________站没有人上车，第_________站没有人下车；
（3）中间第二站开车时车上人数是_______人，第五站停车时车上人数是_________人；
（4）从表中你还能知道的一个信息是_________
已知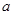
、
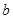互为相反数且
，
、
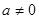互为倒数，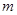
的绝对值是最小的正整数，
求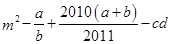
的值． （注：
=
）
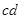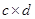解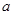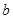：∵、互为相反数且， ∴
__________，
__________；
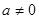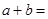又∵、互为倒数，∴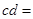
__________；
又∵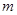的绝对值是最小的正整数， ∴
__________，∴
__________；
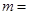∴原式
__________．
某检修小组从A地出发，在东西方向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶记录如下（单位：千米）:
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| －3 |
+8 |
－9 |
+10 |
+4 |
－6 |
－2 |
（1）在第几次行驶时距A地最远？
（2）收工时距A地多远？
（3）若每千米耗油0．3升，每升汽油需7．2元，问检修小组工作一天需汽油费多少元？
观察下列等式
，
，
，
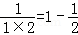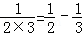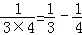将以上三个等式两边分别相加得：
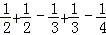=1﹣
=1﹣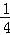
=
．
（1）猜想并写出：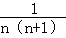
．
（2）根据以上规律直接写出下列各式的计算结果：
①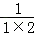
+
+
+…+
= ；
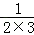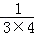②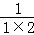
+
++…+
．
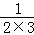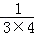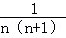（3）探究并计算：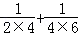
+
+…+
．
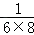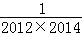观察下列各式：
﹣1×
=﹣1+
﹣×
=﹣+
﹣×
=﹣
+
…
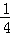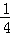
（1）你能探索出什么规律？（用文字或表达式）
（2）试运用你发现的规律计算：
（﹣1×
）+（﹣×）+（﹣×）+…+（﹣
×
）+（﹣×
）
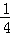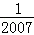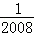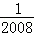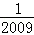10名学生体检测体重，以50千克为基准，超过的数记为正，不足的数记为负，称得结果如下（单位：千克）
2，3，﹣7.5，﹣3，5，﹣8，3.5，4.5，8，﹣1.5．这10名学生的总体重为多少？平均体重为多少？
；
（用简便方法）．
的意义是
．
．
的值．
时，
值．
．例如：
,请用上述规定计算下面各式：
；
．
粤公网安备 44130202000953号