一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
计算:
(1)(﹣2)2×7﹣62÷(﹣3)×
(2)先化简,再求值:2(a2b+ab2)﹣2(a2b﹣1)﹣3ab2+2,其中a=﹣2,b=2.
观察下列各式:
13+23= ;
;
13+23+33=36= ;
;
13+23+33+43=100= ;
;
(1)计算:13+23+33+43+53的值;
(2)计算:13+23+33+43+…+103的值;
(3)猜想:13+23+33+43+…+n3的值.
图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n= .
.

如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度0.45元收费,如果超过140度,超过部分按每度0.60元收费.
(1)若该住户五月份的用电量是100度,则他五月份应交多少电费?
(2)若该住户六月份的用电量是200度,则他六月份应交多少电费?
(3)若某住户七月份的用电量是 度(
度( >140),求这个用户七月份应交多少电费?(结果用含
>140),求这个用户七月份应交多少电费?(结果用含 的式子表示)
的式子表示)
某检修小组从A地出发,在东西朝向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:km)
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| ﹣4 |
+7 |
﹣9 |
+8 |
+6 |
﹣5 |
﹣2 |
(1)求收工时距A地多远?
(2)若每km耗油0.3升,问共耗油多少升?
已知10箱苹果,以每箱15千克为标准,超过15千克的数记为正数,不足15千克的数记为负数,称重记录如下:+0.2,﹣0.2,+0.7,﹣0.3,﹣0.4,+0.6,0,﹣0.1,+0.3,﹣0.2(本题6分)
(1)求10箱苹果的总重量;
(2)若每箱苹果的重量标准为15±0.5(千克),则这10箱有几箱不符合标准的?
为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费多少元?
(2)若某户居民3月份交水费36元,则用水量为多少立方米?
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费.
(4)若某户居民5、6两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该户居民5、6两个月共交水费多少元.
观察下列等式: ,
, ,
, ;将以上三个等式两边分别相加得:
;将以上三个等式两边分别相加得: .
.
(1)猜想并写出: .
.
(2)直接写出下列各式的计算结果:
① ;
;
② .
.
(3)探究并计算式子: 的值.
的值.
仔细观察下列三组数:
第一组:1,4,9,16,25,…
第二组:1,8,27,64,125,…
第三组:﹣2,﹣8,﹣18,﹣32,﹣50,…
(1)写出每组的第6个数各是多少?
(2)第二组的第100个数是第一组的第100个数的多少倍?
(3)取每组数的第n个数,计算这三个数的和.
某一食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
这批样品的平均质量比标准质量多还是少?多或少几克,若标准质量为450克,则抽样检测的总质量是多少?
有一批水果,包装质量为每筐25千克,现抽取10筐样品进行检测,结果称重如下(单位:千克):21,24,27,28,25,26,22,23,25,26为了求得10筐样品的总质量,我们可以选取一个恰当的基准数进行简化运算.
| 原质量 |
21 |
24 |
27 |
28 |
25 |
26 |
22 |
23 |
25 |
26 |
| 与基准数的差距 |
|
|
|
|
|
|
|
|
|
|
(1)你认为选取的一个恰当的基准数为____________;
(2)根据你选取的基准数,用正、负数填写上表;
(3)这10筐水果的总质量是多少千克?
已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=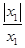 ,则
,则 = ;
= ;
(2)若y2= ,则
,则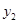 = ;
= ;
(3)若y3=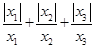 ,则
,则 = ;
= ;
(4)由以上探究可知,y2012= ,
,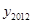 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
下图是一个数字转换机,请解答下列问题:

(1)填空:若输入的x值为2,则输出的y值为
(2)若输入的x值为1,则输出的y值为
(3)若输出的y值为28,那么输入的x值是什么?(写出三个x值,并写出简要的分析过程.)
有20筐白菜,以每筐25千克为标准,超过千克数记为正数,不足的千克数记为负数,记录如表:
| 与标准质量的差值(单位:千克) |
-3 |
-2 |
-1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
4 |
6 |
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?