初中数学有理数的混合运算解答题

观察下列等式，，，将以上3个等式两边分别相加得， 
①直接写出结果=      ．
②计算：．

某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：

星期	一	二	三	四	五	六	日
增减	+6	-2	-4	+12	-10	+16	-8

 
（1）根据记录的数据可知该厂星期四生产自行车         辆；
（2）产量最多的一天比产量最少的一天多生产自行车           辆；
（3）根据记录的数据可知该厂本周实际生产自行车             辆；
（4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖20元；少生产一辆扣25元，那么该厂工人这一周的工资总额是多少元？

定义新运算．a⊗b=a²-|b|，如3⊗（-2）=3²-|-2|=9-2=7，计算下列各式．
（1）（-2）⊗3
（2）（-3）⊗（0⊗（-1））

为了保护广大消费者的利益，最近工商管理人员在一家面粉店抽查了20袋面粉，称得它们的重量如下（单位：千克）：25，25，24，24，23，24，24，25，26，25，23，23，24，25，25，24，24，26，26，25，请你计算这20袋面粉的总重量和每袋的平均重量，你能找出比较简单的计算方法吗？请你试试，根据你的计算结果，你对这次检查情况有什么看法？（每袋面粉的标准重量为：25千克）

一股民上周末以每股27元价格买了1000股股票，下表为本周内每日股票的涨跌情况（单位：元）：

星期	一	二	三	四	五
涨跌（与前一交易日比较）	+4	+4.5	-1	-2.5	-4

（1）星期四收盘时，每股多少元？
（2）本周内每股最高价，最低价分别是多少元？
（3）已知该股民买进股票时付了百分之零点一五的手续费，卖出时需付成交额百分之零点一五的手续费和百分之零点一的交易税，如果他一直观望到星期五才将股票全部卖出，请你算算他本周的收益如何．

已知a、b互为相反数，c、d互为倒数，m的倒数等于它本身，则的值是多少？

某检修小组乘一辆检修车沿铁路检修，规定向东走为正，向西走为负，小组的出发地记为0，某天检修完毕时，行走记录（单位：千米）如下：
+10，-2，+3，-1，+9，-3，-2，+11，+3，-4，+6．
（1）问收工时，检修小组距出发地有多远？在东侧还是西侧？
（2）若检修车每千米耗油2．8升，求从出发到收工共耗油多少升？

某自行车厂计划每天平均生产n辆自行车，而实际产量与计划产量相比有出入．下表记录了某周五个工作日每天实际产量情况（超过计划产量记为正、少于计划产量记为负）：

星期	一	二	三	四	五
实际生产量	+5	﹣2	﹣4	+13	﹣3

 
（1）用含n的代数式表示本周前三天生产自行车的总数；
（2）该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，当n=100时，那么该厂工人这一周的工资总额是多少元？
（3）若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，当n=100时，在此方式下这一周工人的工资与按日计件的工资哪一个更多？请说明理由．

列式并计算：
（1）﹣1减去的差乘以﹣7的倒数的积；
（2）﹣2、5、﹣9这三个数的和的绝对值比这三个数的绝对值的和小多少？

已知a的相反数为-2，b的倒数为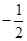，c的绝对值为2，求a+b+c²的值．

我们规定“*”是一种数学运算符号，两数A、B通过“*”运算得（A+2）×2-B，即A*B=（A+2）×2-B，例如，3*5=（3+2）×2-5=5
（1）求6*7的值；
（2）6*7的值与7*6的值相等吗？

某市区自2014年1月起，居民生活用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：

月用水量（吨）	水价（元/吨）
第一级 20吨以下（含20吨）	1．6
第二级 20吨﹣30吨（含30吨）	2．4
第三级 30吨以上	3．2

 
例：某用户的月用水量为32吨，按三级计量应缴水费为：
1．6×20＋2．4×10＋3．2×2＝62．4（元）
（1）如果甲用户的月用水量为12吨，则甲需缴的水费为       元；
（2）如果乙用户缴的水费为39．2元，则乙月用水量         吨；
（3）如果丙用户的月用水量为a吨，则丙用户该月应缴水费多少元？（用含a的代数式表示，并化简）

出租车司机小李某天下午的营运全是在东西走向的城中路上进行的，如果规定向东行驶为正，他这天下午行车的里程（单位：千米）如下：＋8， －7， ＋10， －6，＋3，－5，＋9，－6
（1）小李下午出发地记为0，他将最后一名乘客送抵目的地时，小李在出发地的什么方向？距下午出发地有多远？
（2）如果汽车耗油量为0．5升/千米，油箱容量为26升，若出发时油箱装满汽油，请你判断途中是否需要补充汽油？

有一批水果，包装质量为每筐25千克，现抽取8筐样品进行检测，结果称重如下（单位：千克）：27，24，23，28，21，26，22，27，为了求得8筐样品的总质量，我们可以选取的一个恰当的基准数进行简化运算．
（1）你认为选取的一个恰当的基准数为          ；
（2）根据你选取的基准数，用正、负数填写上表；

原质量	27	24	23	28	21	26	22	27
与基准数的差距

 
（3）这8筐水果的总质量是多少？

出租车司机小傅某天下午营运全是在东西走向的大道上行驶的．若如果规定向东为正，则行车里程（单位：km）如下：
＋11，－2，＋3，＋10，－11，＋5，－15，－8
（1）当把最后一名乘客送到目的地时，小傅距离出车地点的距离为多少？
（2）若每千米的营运额为7元，成本为1．5元/km，则这天下午他盈利多少元？