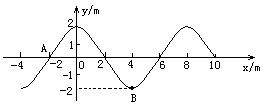
如图为某时刻t的横波图像,求:
(1)这列波的波长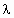 和振幅A;
和振幅A;
(2)若波沿x轴正方向传播,当波速为4m/s时,经1s时,A点位移是多大?B点通过的路程是多少?
(3)画出(t+0.5)s时的波形图;
(4)画出x=6m处的质点从此刻(t时刻)起的振动图像.
溜冰的小孩站在冰面上靠着固定的木桩推出一冰车,可使冰车获得速度v,若他站在冰面上推出这一冰车,在做功相同的条件下,冰车可获的速度大小为多大.(冰面阻力不计)

如图,一绳绕过两个滑轮,一端系着质量为M的重物,另一端系着质量为m的浮于水上的小船,开始时小船静止,并设法使重物也静止.释放重物后,重物下降一段距离到达p处时,小船的速度为υ,此时系在船上的斜绳与水平方向所夹的锐角为θ.若不计滑轮、绳的质量及一切阻力,求上述过程中重力对质量为M的重物做的功。
把质量为2kg的物体竖直向上抛出,初速度是12m/s,经1s物体到达所能达到的最高点.设空气阻力大小不变,则前2s内物体重力势能的增加量是多大?空气阻力对物体做了多少功?(g取10m/ )
)

如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R.一个质量为m的静止物块在A处压缩弹簧,在弹力的作用下获某一向右速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点.求:
(1)弹簧的弹力对物块做的功;
(2)物块从B至C克服阻力做的功;
(3)物块离开C点后落回水平面时动能的大小.

如图所示,在竖直平面内有一个固定的、半径为R的半圆形轨道.一质量为m、可视为质点的物体自轨道的最高点A沿轨道无初速地滑下,物体与轨道之间的动摩擦因数为μ.当物体滑到最低点B时的速度是假如在无摩擦情况下滑到B点时速度的一半.求经过B点时,物体受到的摩擦力的大小.
质量为的小车在光滑的水平轨道上匀速向右运动,速度为
。在小车下方中心
处悬挂一根长长的轻绳,绳下端拴一个质量
的钢块,钢块随小车一起运动,轻绳保持竖直方向,如图所示。一颗质量为
的子弹从左边沿水平方向向右射来,速度为
,与钢块发生碰撞,碰撞时间极短,碰后子弹以
的速度反向弹回。求钢块在此后的运动过程中离最低点的高度的最大值。


如图所示,一根轻杆长为2 l, 它的左端O点为固定转动轴, 轻杆可以绕 O轴在竖直平面内无摩擦转动, 它的中点及右端各固定一个小球A和B, 两球的质量分别是m和 2 m , 重力加速度为g。现用外力使杆处于水平位置, 从静止释放。求从开始运动到达杆处于竖直位置的过程中, 杆的作用力对B球所做的功。
蹦床运动是一种新兴的体育项目,运动员在下落弹起的过程中可做出各种高难的体操动作,显示人的健康美.若某位运动员从3.2m处下落,被弹起升到4.05m,其历时2.2s,运动员质量为60kg,试分析:
(1)运动员和蹦床面之间的平均作用力是多大?
(2)忽略空气阻力及蹦床阻力时,运动员在与蹦床接触过程中做了多少功?
(3)运动员在全过程中共经历了几个运动过程?

如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R、A端与圆心O等高,AD为水平面,B端在O的正上方,一个小球自A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达B点,求:
(1)释放点距A点的竖直高度;
(2)落点C与A点的水平距离;

质量为0.4kg的小物体固定在直棒的一端,棒长为1.0m,,其重力不计,使其形成一个摆,该物体被推向一侧直到棒与竖直线成53°角.试问:(1)小物体应以多大的切向速率VA从A点出发,才能达到最高点C时具有切向速率3m/s?(2)小物体以速度VA从A点出发时,通过最低点B时的速率是多大? (3)若小物体以(1)中的速率VA从A点出发,但方向却相反,它到达C点的速率是多少?(4)若以同样长的绳子代替直棒,小物体仍以(1)中的条件出发,到达某一点D时绳子中的张力为零?(5)在D点时的速率是多少?(6)过D点后小物体的运动情况将如何?

某人要把边长为l=80cm、质量均匀分布、重为G=600N的立方体搬运到高为1.44m的载重卡车上去,他靠车边固定一块硬板,板与水平地面成37°角,现重物停放在斜板旁边,如图所示。他采用翻滚的办法,即先使重物以图中过d点的边为轴顺时针转90°角,然后再依次翻转,直至转到车上。已知重物在板上没有滑动,在这整个过程中他至少要做多少功?
把打桩机的重锤从离桩顶端2.0m高处自由下落,打到桩上,锤与桩的作用时间极短,作用后锤不弹起而与桩一起运动,桩被打入土中20cm深停止。如果桩受到地面的阻力大小跟它进入土中的深度成正比,并且桩受到土的阻力比桩和锤的重力要大得多。那么再把重锤升到原高度自由落下,这次打击能把桩再打入土中多深?