质量为1kg的物体,当t=0时,初速度为零,并处在坐标原点位置,从t=0开始受到一个沿x轴正方向呈周期性变化的外力作用(不再考虑其他力的作用),力变化情况如右图所示。求:
(1)2s末时物体的速度大小?
(2)前3s内物体的位移大小?
如图所示,竖直墙面与水平地面均光滑且绝缘。两个带有同种电荷的小球A、B分别位于竖直墙面和水平地面上,且处于同一竖直平面内。若用图示方向的水平推力F作用于小球B,则两球静止于图示位置。如果将小球B向左推动少许,并待两球重新达到平衡时,与原来相比( )
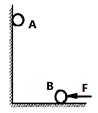
A.两小球的间距变大 B.B球受到的推力F变大
C.A球对竖直墙面的压力变小 D.水平地面给B球的支持力不变
如图所示,虚线框abcd内为边长均为L的正方形匀强电场和匀强磁场区域,电场强度的大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷量为e的电子(重力不计)从PQ中点与PQ成30°角以不同的初速度射入磁场,求: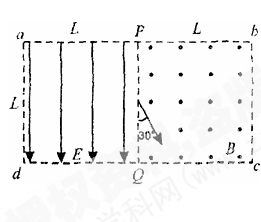
(1)能从PQ边离开磁场的电子在磁场运动的时间.
(2)若要电子在磁场运动时间最长,其初速v应满足的条件?
(3)若电子在满足(2)中的条件下且以最大速度进入磁场,最终从电场aP边界飞出虚线框所具有的动能EK。
如图所示,从电子枪射出的电子束(初速度不计)经电压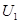 =2000V加速后,从一对金属板Y和Y′正中间平行金属板射入,电子束穿过两板空隙后最终垂直打在荧光屏上的O点。若现在用一输出电压为
=2000V加速后,从一对金属板Y和Y′正中间平行金属板射入,电子束穿过两板空隙后最终垂直打在荧光屏上的O点。若现在用一输出电压为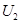 =160V的稳压电源与金属板Y、Y′连接,在YY′间产生匀强电场,使得电子束发生偏转.设电子质量m=9×
=160V的稳压电源与金属板Y、Y′连接,在YY′间产生匀强电场,使得电子束发生偏转.设电子质量m=9×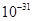 kg,电量e=1.6×
kg,电量e=1.6×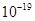 C,YY′两板间距d=2.4cm,板长l=6.0cm,板的末端到荧光屏的距离L=12cm。整个装置处于真空中,不考虑电子重力及电子间相互作用。试求:
C,YY′两板间距d=2.4cm,板长l=6.0cm,板的末端到荧光屏的距离L=12cm。整个装置处于真空中,不考虑电子重力及电子间相互作用。试求: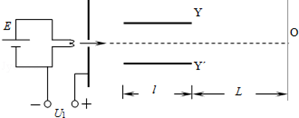
(1)电子束射入金属板Y、Y′时速度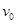 =?
=?
(2)电子束离开金属板Y、Y′时,偏离入射方向的竖直位移量y=?
(3)如果两金属板Y、Y′间的距离d可以随意调节(保证电子束仍从两板正中间射入),其他条件都不变,那么电子束打到荧光屏上的位置P(图中未标出)到O点的距离是否存在最大值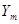 ?如果存在
?如果存在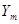 =?(第3问只需写出结果,不必写详细解题过程。)
=?(第3问只需写出结果,不必写详细解题过程。)
水平面上有电阻不计的U形导轨NMPQ,它们之间的宽度为L,M和P之间接入电动势为E的电源(不计内阻).现垂直于导轨搁一根质量为m,电阻为R的金属棒ab,并加一个范围较大的匀强磁场,磁感应强度大小为B,方向与水平面夹角为θ且指向右斜上方,如图所示,问:
(1)当ab棒静止时,受到的支持力和摩擦力各为多少?
(2)若B的大小和方向均能改变,则要使ab棒所受支持力为零,B的大小至少为多少?此时B的方向如何?
如图所示,在匀强电场中,将一电荷量为2×10-5的负电荷由A点移到B点,其电势能增加了0.1J,已知A、B两点间距离为2cm,两点连线与电场方向成600角,求: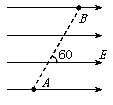
(1) 电荷由A移到B的过程中,电场力所做的功WAB;
(2) A、B两点间的电势差UAB;
(3) 该匀强电场的电场强度E。
如图,灯泡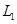 :1.0V 0.5W;
:1.0V 0.5W;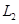 :10V 1.0W;电动机内阻5.0Ω.此时两灯泡都刚好正常发光,电动机也在正常运转,求电动机的输出功率和效率.
:10V 1.0W;电动机内阻5.0Ω.此时两灯泡都刚好正常发光,电动机也在正常运转,求电动机的输出功率和效率.
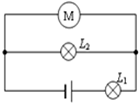
如图所示,平行板电容器的板长为L,板间距离为d,板B与水平方向的夹角为α,两板间所加电压为U,有一带负电液滴,带电量为q,以速度 沿水平方向自A板边沿进入板间后仍沿水平方向运动,恰好从B板沿水平飞出,求液滴的质量及飞出时的速度(重力加速度为g)
沿水平方向自A板边沿进入板间后仍沿水平方向运动,恰好从B板沿水平飞出,求液滴的质量及飞出时的速度(重力加速度为g)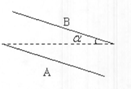
频闪照相是研究物理过程的重要手段,如图所示是某同学研究一质量为m=0.5kg的小滑块从光滑水平面滑上粗糙斜面并向上滑动时的闪频照片,已知斜面足够长,倾角为α=37°,闪光频率为10Hz经测量换算获得实景数据, ,
,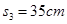 ,
,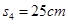 ,取
,取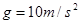 ,sin37°=0.6,cos37°=0.8,设滑块通过平面与斜面连接处时没有能力损失,求:
,sin37°=0.6,cos37°=0.8,设滑块通过平面与斜面连接处时没有能力损失,求: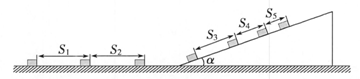
(1)滑块与斜面间的动摩擦因数为μ,并说明滑块在斜面上运动到最高点后能否自行沿斜面下滑;
(2)从滑块滑上斜面开始计时,经过长时间到达斜面上的A点(图中A点未画出,已知A点到斜面最低点B的距离为0.6m)。(注意:结果可以用根号表示)
如图所示,带有小孔的平行板极板A.B间存在匀强电场,电场强度为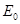 ,极板间距离为L,其右侧有与A.B垂直的平行极板C.D,极板长度为L,C.D板加不变电压。现有一质量为m,带电量为e的电子(重力不计),从A板处由静止释放,经电场加速后通过B板的小孔飞出,经C.D板间的电场偏转后从电场的右侧边界M点飞出电场区域,速度方向与边界夹角为60°,求:
,极板间距离为L,其右侧有与A.B垂直的平行极板C.D,极板长度为L,C.D板加不变电压。现有一质量为m,带电量为e的电子(重力不计),从A板处由静止释放,经电场加速后通过B板的小孔飞出,经C.D板间的电场偏转后从电场的右侧边界M点飞出电场区域,速度方向与边界夹角为60°,求: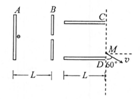
(1)电子在A.B间的运动时间;
(2)C.D间匀强电场的电场强度。
如图所示,在第一象限有一匀强电场,场强大小为E,方向与y轴平行;在x轴下方有一匀强磁场,磁场方向与纸面垂直,一质量为m,电荷量为-q(q>0)的粒子以平行于x轴的速度从y轴上的P点处射入电场,在x轴上的Q点处进入磁场,并从坐标原点O离开磁场,粒子在磁场中的运动轨迹y轴交与M点,已知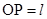 ,
,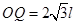 。不计重力,求:
。不计重力,求: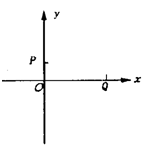
(1)M点与坐标原点O间的距;
(2)粒子从P点运动到M点所用的时间。
如图所示,有一区域足够大的匀强磁场,磁感应强度为B,磁场方向与水平放置的导轨垂直,导轨宽度为L,右端接有电阻R,MN是一根质量为m的金属棒,金属棒与导轨垂直放置,且接触良好,金属棒与导轨电阻均不计,金属棒与导轨间的动摩擦因数为μ,现给金属棒一水平冲量,使它以初速度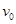 沿导轨向左运动,已知金属棒在整个运动过程中,通过任一截面的总电荷量为q,求:
沿导轨向左运动,已知金属棒在整个运动过程中,通过任一截面的总电荷量为q,求: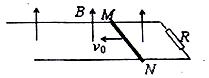
(1)金属棒运动的位移s;
(2)金属棒运动过程中回路产生的焦耳热Q;
(3)金属棒运动的时间t
如图所示,在冰面上将质量m=1kg的滑块从A点以初速度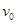 推出,滑块与冰面的动摩擦因数为
推出,滑块与冰面的动摩擦因数为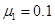 ,滑块滑行L=18m后到达B点时速度为
,滑块滑行L=18m后到达B点时速度为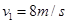 ,现将期间的一段CD用铁刷划擦,使该段的动摩擦因数变为
,现将期间的一段CD用铁刷划擦,使该段的动摩擦因数变为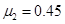 ,再使滑块从A以
,再使滑块从A以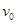 的初速度推出后,到达B点的速度为
的初速度推出后,到达B点的速度为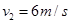 ,取
,取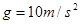 ,求:
,求:
(1)初速度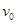 的大小;
的大小;
(2)CD段的长度l;
(3)若AB间用铁刷划擦的CD段的长度不变,要使滑块从A到B的运动时间最长,问铁刷划擦的CD段位于何位置?并求滑块滑行的最长时间(结果保留三位有效数字)。
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍,利用双星系统中两颗恒星的运动特征可推算出它们的总质量。已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量。(引力常量为G)