高中物理计算题

如下图所示，在空间有一直角坐标系xOy，直线OP与x轴正方向的夹角为30°，第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ，直线OP是它们的理想边界，OP上方区域Ⅰ中磁场的磁感应强度为B。一质量为m、电荷量为q的质子（不计重力，不计质子对磁场的影响）以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ，质子先后通过磁场区域Ⅰ和Ⅱ后，恰好垂直打在x轴上的Q点（图中未画出）。试求：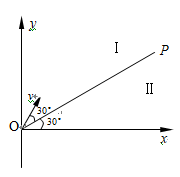

（1）区域Ⅱ中磁场的磁感应强度大小；
（2）Q点到O点的距离。

如下图所示的电路中，已知电阻R₁=9Ω，R₂=15Ω，电源的电动势E=12V，内电阻r=1Ω，电流表的读数I=0.4A。求电阻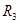的阻值和它消耗的电功率；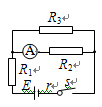

如右图所示，一质量m=1×10^-6kg，带电量q=－2×10^-8C的微粒以初速度v₀竖直
向上从A点射入一水平向右的匀强电场，当微粒运动到比A高2cm的
B点时速度大小也是v₀，但方向水平，且AB两点的连线与水平方向的
夹角为45º，g取10m/s²。求：

（1）AB两点间的电势差U_AB；
（2）匀强电场的场强E的大小。

如图所示，在平面直角坐标系xOy中，第一象限内存在正交的匀强电磁场，电场强度E₁=40N/C；第四象限内存在一方向向左的匀强电场。一质量为m=2×10^-3kg带正电的小球，从M（3.64m，3.2m）点，以v₀=1m/s的水平速度开始运动。已知球在第一象限内做匀速圆周运动，从P（2.04m，0）点进入第四象限后经过y轴上的N（0，-2.28m）点（图中未标出）。（g=10m/s²，sin37°=0.6，cos37°=0.8）求：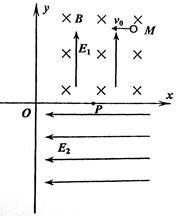

（1）匀强磁场的磁感应强度B
（2）小球由P点运动至N点的时间

如图所示，“”型平行金属导轨，倾角=37⁰，导体棒MN、PQ分别与导轨垂直放置，质量分别为m₁和m₂，MN与导轨的动摩擦因数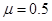，PQ与导轨无摩擦，设最大静摩擦力等于滑动摩擦力，装置整体置于方向垂直倾斜导轨平面向上的匀强磁场中，现将导体棒PQ由静止释放（设PQ离底端足够远）。试分析m₁与m₂应该满足什么关系，才能使导体棒MN在导轨上运动。

如图所示，一质量为1kg的小物块静止于水平地面上A点，在一恒定拉力作用下，经2s运动到B点后撤去拉力，小物块恰好滑上与地面等高的传送带上。传送带以恒定速率v₀=4m/s运行，已知AB间距离为x=2m，传送带长度（即BC间距离）为L=10m，物块与传送带间的滑动摩擦因数。

（1）物块在传送带上运动的时间。（g=10m/s²）
（2）物块滑上传送带后，传动系统因此而多消耗的电能。

一辆质量为2吨的汽车由静止开始沿一倾角为30⁰的足够长斜坡向上运动，汽车发动机的功率保持48kW不变，行驶120m后达到最大速度。已知汽车受到地面的摩擦阻力为2000N。（g=10m/s²）求：
（1）汽车可以达到的最大速度
（2）汽车达到最大速度所用的时间（结束保留一位小数）

如图所示，质量为M=8kg的小车放在光滑的水平面上，在小车左端加一水平推力F=8N，当小车向右运动的速度达到v₀=1.5m/s时，在小车前端轻轻放上一个大小不计、质量为m=2kg的小物块，物块与小车间的动摩擦因数μ=0.2。已知运动过程中，小物块没有从小车上掉下来，取g=10m/s²。求：

（1）放上小物块后，经过多长时间两者达到相同的速度？
（2）从小物块放上小车开始，经过t=1.5s小物块通过的位移大小为多少？

如图所示，在倾角为θ=37°的足够长的固定斜面上，有一质量m=1kg的物体，物体与斜面间的动摩擦因数为μ=0.2，物体受到沿斜面向上的拉力F=9.6N的作用，从静止开始运动，经过2s撤去拉力。试求撤去拉力后多长时间物体速度大小可达22m/s。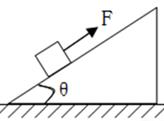

在十字路口，汽车以 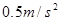的加速度从停车线启动做匀加速运动，刚好有一辆自行车以的速度匀速驶过停车线与汽车同方向行驶，求：
（1）什么时候它们相距最远？最远距离是多少？
（2）汽车追上自行车时，汽车的速度是多大？

在倾角为α的斜面上，一条质量不计的皮带一端固定在斜面上端，另一端绕过一中间有一圈凹槽的圆柱体，并用与斜面夹角为β的力F拉住，使整个装置处于静止状态，如图所示．不计一切摩擦，圆柱体质量为m，求拉力F的大小和斜面对圆柱体的弹力F _N 的大小．

某同学分析过程如下：
将拉力F沿斜面和垂直于斜面方向进行分解．
沿斜面方向：Fcos β＝mgsin α  ①
沿垂直于斜面方向：Fsin β＋F _N ＝mgcos α ②
问：你同意上述分析过程吗？若同意，按照这种分析方法求出F及F _N 的大小；若不同意，指明错误之处并求出你认为正确的结果．

一个滑雪者，质量m=75kg,以v ₀ =2m/s的初速度沿山坡匀加速下滑，山坡的倾角 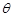=30°，在t=5s的时间内滑下的路程x=60m,求滑雪者受到的阻力（包括摩擦力和空气阻力）。

许多汽车司机喜欢在驾驶室悬挂一些祝福“平安”的小工艺品。如下图所示，沿水平方向做匀变速直线运动的车厢中，悬挂小工艺品的悬线偏离竖直方向37°角，球和车厢相对静止，球的质量为1kg。（ g ＝10m/s ² ，sin37°＝0.6，cos37°＝0.8）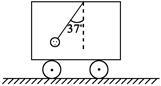

（1）求车厢运动的加速度，并说明车厢的运动情况；
（2）求悬线对球的拉力。

如下图所示，一块质量为M = 2kg，长L = 1m的匀质木板放在足够长的光滑水平桌面上，初始时速度为零．板的最左端放置一个质量m = 1kg的小物块，小物块与木板间的动摩擦因数为μ = 0.2，小物块上连接一根足够长的水平轻质细绳，细绳跨过位于桌面边缘的定滑轮（细绳与滑轮间的摩擦不计，木板与滑轮之间距离足够长，g = 10m/s²，计算结果保留三位有效数字）。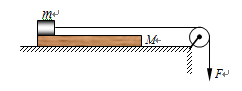

（1）若木板被固定，某人以恒力F = 4N向下拉绳，则小木块滑离木板所需要的时间是多少？
（2）若木板不固定，某人仍以恒力F = 4N向下拉绳，则小木块滑离木板所需要的时间是多少？
（3）若人以恒定速度v₁=1m/s向下匀速拉绳，同时给木板一个v₂ = 0.5m/s水平向左的初速度，则木块滑离木板所用的时间又是多少？

如右图所示，光滑斜面体的质量为M 、斜角为θ ，放置在光滑水平面上，要使质量为m的物体能静止在光滑斜面体上，应对光滑斜面体施以多大的水平外力F？此时m 与 M 之间的相互作用力 F_N为多大？