我国发射的“神州六号”载人飞船，与“神州五号”飞船相比，它在更高的轨道上绕地球做匀速圆周运动，如图所示，下列说法中正确的是（ ）
| A．“神州六号”的线速度较小 |
| B．“神州六号”的线速度与“神州五号”的相同 |
| C．“神州六号”的周期更短 |
| D．“神州六号”的周期与“神州五号”的相同 |
2007年9月24日，“嫦娥一号“探月卫星发射升空，实现了中华民族千年奔月的梦想.“嫦娥一号”卫星在距月球表面200 krn、周期127 min的圆形轨道上绕月球做匀速圆周运动.已知月球半径约为1 700 km，引力常量
，忽略地球对“嫦娥一号”的引力作用.由以上数据可以估算出的物理量有 （ ）
| A．月球的质量 | B．卫星的质量 |
| C．月球表面的温度 | D．月球绕地球公转的周期 |
万有引力定律揭示了天体运动规律与地上物体运动规律具有内在的一致性。
（1）用弹簧秤称量一个相对于地球静止的小物体的重量，随称量位置的变化可能会有不同的结果。已知地球质量为M，自转周期为T，万有引力常量为G．将地球视为半径为R、质量均匀分布的球体，不考虑空气的影响．设在地球北极地面称量时，弹簧秤的读数是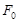
a．若在北极上空高出地面h处称量，弹簧秤读数为
，求比值
的表达式，并就
的情形算出具体数值（计算结果保留两位有效数字）；
b．若在赤道地面称量，弹簧秤读数为
，求比值
的表达式．
（2）设想地球绕太阳公转的圆周轨道半径为r、太阳的半径为
和地球的半径R三者均减小为现在的
，而太阳和地球的密度均匀且不变．仅考虑太阳和地球之间的相互作用，以现实地球的1年为标准，计算“设想地球”的一年将变为多长？
未来“嫦娥五号”落月后，轨道飞行器将作为中继卫星在绕月轨道上做圆周运动，如图所示．设卫星距离月球表面高为h，绕行周期为T，已知月球绕地球公转的周期为T0，地球半径为R，地球表面的重力加速度为g，月球半径为r，万有引力常量为G．试分别求出：
（1）地球的质量和月球的质量；
（2）中继卫星向地球发送的信号到达地球，最少需要多长时间？（已知光速为c，且h≤r≤R）
如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片，该系统是由一颗白矮星和它的类日伴星组成的双星系统，图片下面的亮点为白矮星，上面的部分为类日伴星（中央的最亮的为类似太阳的天体）。由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加，科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”，从而变成一颗超新星。现假设类日伴星所释放的物质被白矮星全部吸收，并且两星之间的距离在一段时间内不变，两星球的总质量不变，不考虑其它星球对该“罗盘座T星”系统的作用，则下列说法正确的是（ ）
| A．两星之间的万有引力不变 |
| B．两星的运动周期不变 |
| C．类日伴星的轨道半径减小 |
| D．白矮星的线速度变小 |
P1、P2为相距遥远的两颗行星，距各自表面相同高度处各有一颗卫星S1、S2做匀速圆周运动，图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a，横坐标表示物体到行星中心的距离r的平方，两条曲线分别表示P1、P2周围的a与r2的反比关系，它们左端点横坐标相同，则 （ ）
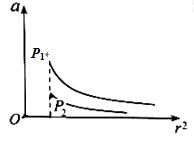
| A．P1的第一宇宙速度比P2的大 |
| B．P1的密度比P2的密度小 |
| C．S1的向心加速度比S2的小 |
| D．S1的公转周期比S2的大 |
假设地球可视为质量分布均匀的球体。已知地球表面两极处的重力加速度大小为g0，地球的半径为R，地球的自转周期为T，引力常量为G，由此可知（ ）
A．地球的质量为 |
B．地球表面赤道处的重力加速度大小为 |
| C．近地卫星在轨运行的加速度大小为g0 |
D．地球同步卫星在轨道上运行的加速度大小为 |
“神六升空，双雄巡天”，真正实现了中国人参与外层空间科学实验的梦想．已知地球半径为R，地球表面的重力加速度为g．
（1）飞船入轨后沿椭圆轨道运动，其远地点离地面高度为地球半径的
，则该处的重力加速度是多大？
（2）假设“神舟六号”飞船绕地球飞行过程中沿圆轨道运行，周期为T，则飞船离地面的高度是多少？
迄今发现的二百余颗太阳系外行星大多不适宜人类居住，绕恒星“Gliese581”运行的行星“G1﹣58lc”却很值得我们期待．该行星的温度在O℃到40℃之间、质量是地球的6倍、直径是地球的1.5倍、公转周期为13个地球日．“Gliese581”的质量是太阳质量的0.31倍．设该行星与地球均视为质量分布均匀的球体，绕其中心天体做匀速圆周运动，则（ ）
| A．在该行星和地球上发射卫星的第一宇宙速度相同 |
B．如果人到了该行星，其体重是地球上的 倍 |
C．该行星与“Gliese581”的距离是日地距离的 倍 |
| D．由于该行星公转速率比地球大，地球上的米尺如果被带上该行星，其长度一定会变短 |
某人造地球卫星绕地球做匀速圆周运动，它离地面的高度为地球半径R的3倍，已知地面附近的重力加速度为g，引力常量为G．求：
（1）地球的质量；
（2）这颗人造地球卫星的向心加速度和周期．
地球的质量是月球的81倍，地球与月球之间的距离为S，某飞行器运动到地球与月球连线的某位置时，地球对它吸引力大小是月球对它吸引力大小的4倍，则此飞行器离地心的距离是（ ）
A． |
B． |
C． |
D． |
如图所示，飞行器P绕某星球做匀速圆周运动，星球相对飞行器的张角为
，下列说法正确的是
| A．轨道半径越大，周期越长 |
| B．张角越大，速度越大 |
| C．若测得周期和张角，则可得到星球的平均密度 |
| D．若测得周期和轨道半径，则可得到星球的平均密度 |
如右图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间的距离为L。已知A、B的中心和O三点始终共线，A和B分别在O的两侧。引力常数为G。
（1）求两星球做圆周运动的周期
（2）在地月系统中，若忽略其他星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期为
。但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期记为
。已知地球和月球的质量分别为
和
。求与两者平方之比。（结果保留3位小数）
如图所示，曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图，其半径为R；曲线Ⅱ是绕地球做椭圆运动卫星2的轨道示意图，O点为地球的地心，AB为椭圆的长轴，两轨道和地心都在同一平面内，已知在两轨道上运动的卫星的周期相等，万有引力常量为G，地球质量为M，下列说法正确的是（ ）
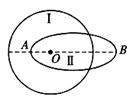
| A．椭圆轨道长轴AB的长度为R |
B．在Ⅰ轨道的卫星1的速率为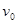 ，在Ⅱ轨道的卫星2通过B点的速率为 ， |
C．在Ⅰ轨道的卫星1的加速度大小为 ，在Ⅱ轨道的卫星2通过A点的加速度大小为 ， |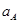
D．若OA=0.5R，则卫星在B点的速率 |
处的重力加速度大小与在地面下方地球内部离地面距离为
粤公网安备 44130202000953号