高中物理万有引力定律及其应用试题

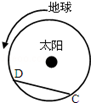
如图所示设地球的质量为M且绕太阳做匀速圆周运动，当地球运动到D点时，有一质量为m的飞船由静止开始从D点只在恒力F的作用下沿DC方向做匀加速直线运动，再过两个月，飞船在C处再次掠过地球上空，假设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向，飞船到地球表面的距离远小于地球与太阳间的距离，则地球与太阳间的万有引力大小（ ）

A．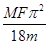

B．

C．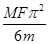

D．

2015年8月27日10时31分，我国在太原卫星发射中心用长征四号丙运载火箭，成功将遥感二十七号卫星送人太空。若遥感二十七卫星到地面的距离等于地球的半径R，已知地球表面的重力加速度为g。求遥感二十七号卫星的周期T。

如图，A为太阳系中的天王星，它绕太阳O运行的轨道视为圆时，运动的轨道半径为R₀，周期为T_o人匀速圆周运动。天文学家长期观测发现，天主星实际运动的轨道与圆轨道总有一些偏离，且每隔t_o时间发生一次最大偏离，形成这种现象的原因可能是夭王星外侧还存在着一颗未知的行星B，假设行星B与A在同一平面内，且与A的绕行方向相同，它对天王星的万有引力引起天王星轨道的偏离，由此可推测未知行星的运动轨道半径是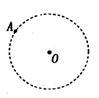

A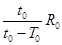．	B．
C．	D．

2014年3月8日凌晨马航客机失联后，西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星，为地面搜救提供技术支持。特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术。如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图，“北斗系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动，卫星“G1”和“G3”的轨道半径均为r，某时刻两颗工作卫星分别为轨道上的A.B两位置，高分一号在C位置，若卫星均顺时针运行，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力。则以下说法正确的是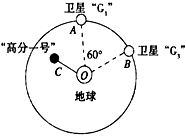

A.卫星“G1”和“G3”的加速度大小相等均为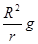
B.卫星“G1”由位置A运动到位置B所需要的时间为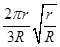
C.如果调动“高分一号”卫星到达卫星“G3”所在的轨道，必须对其减速
D.高分一号是低轨道卫星，其所在高度由稀薄气体，运行一段时间后，高度会降低，速度增大，机械能会减小

2015年8月27日10时31分，我国在太原卫星发射中心用长征四号丙运载火箭，成功将遥感二十七号卫星送人太空。若遥感二十七卫星到地面的距离等于地球的半径R，已 知地球表面的重力加速度为g。求遥感二十七号卫星的周期T。

“嫦娥二号”是我国月球探测第二期工程的先导星．若测得“嫦娥二号”在月球(可视为密度均匀的球体)表面附近圆形轨道运行的周期为T，已知引力常量为G，半径为R的球体体积公式V＝πR³，则可估算月球的(  )．

A．半径

B．质量

C．密度

D．自转周期

“嫦娥一号”卫星开始绕地球在椭圆轨道运动，经过变轨、制动后，成为一颗绕月球做圆周运动的卫星。设卫星距月球表面的高度为h ，做匀速圆周运动的周期为T 。已知月球半径为R ，引力常量为G。求：
（1）月球的质量M及月球表面的重力加速度g；
（2）在距月球表面高度为h₀的地方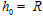（），将一质量为m的小球以v₀的初速度水平抛出，求落地瞬间月球引力对小球做功的瞬时功率P。

我国发射了一颗地球资源探测卫星，发射时，先将卫星发射至距离地面50km的近地圆轨道1上，然后变轨到近地点距离地面50km、远地点距离地面1500km的椭圆轨道2上，最后由轨道2进入半径为7900km的圆轨道3，轨道1、2相切于P点，轨道2、3相切于Q点。忽略空气阻力和卫星质量的变化，则以下说法正确的是（       ）

A．该卫星从轨道1变轨到轨道2需要在P处点火减速

B．该卫星在轨道3的机械能大于在轨道1的机械能

C．该卫星在轨道2上稳定运行时，P点的速度小于Q点的速度

D．该卫星在轨道2上Q点的加速度大于在轨道3上Q点的加速度

2014年最大最圆的“超级月亮”在8月11日凌晨2时前后现身天幕。11日1时42分，月亮运行到近地点，距离地球最近，与远地点相比，可观测到月球面积增大14%，亮度增加30%，月球绕地球运行椭圆轨道abcda如图所示，运行周期为T, a为其近地点、c为远地点，b、d为曲线ac的中点．下列说法正确的是（ ）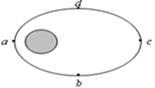

A．月球从a到b再到c的过程中，速率逐渐变小

B．月球从a到b所用时间等于T∕4

C．月球从b到c再到d的过程中，万有引力对它先做负功后做正功

D．月球在a点的机械能大于在b点的机械能

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v₀，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r，周期为T。火星可视为半径为r₀的均匀球体。

试将一天的时间记为T，地球半径记为R，地球表面重力加速度为g．（结果可保留根式）
（1）试求地球同步卫星P的轨道半径R_P；
（2）若已知一卫星Q位于赤道上空且卫星Q运动方向与地球自转方向相反，赤道上一城市A的人平均每三天观测到卫星Q四次掠过他的上空，试求Q的轨道半径R_Q

已知某行星半径为R，以某第一宇宙速度运行的卫星的绕行周期为T，围绕该行星运动的同步卫星运行速率为v，则该行星的自转周期为：

A．

B．

C．

D．

2013年6月，我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接．如图所示，已知“神舟十号”从捕获“天宫一号”到实现对接用时t，这段时间内组合体绕地球转过的角度为θ（此过程轨道不变，速度大小不变），地球半径为R，地球表面重力加速度为g，万有引力恒量G，不考虑地球自转；求：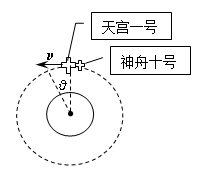

（1）地球质量M；
（2）组合体运动的周期T；
（3）组合体所在圆轨道离地高度H。

2007年10月24日，“嫦娥一号”成功发射，11月5日进入38万公里以外的环月轨道，11月24日传回首张图片，这是我国航天事业的又一成功。“嫦娥一号”围绕月球的运动可以看作匀速圆周运动，万有引力常量已知，如果在这次探测工程中要测量月球的质量，则需要知道的物理量有（  ）

A．“嫦娥一号”的质量和月球的半径

B．“嫦娥一号”绕月球运动的周期和轨道半径

C．月球的半径和“嫦娥一号”绕月球运动的周期

D．“嫦娥一号”的质量、月球的半径和“嫦娥一号”绕月球运动的周期

未来“嫦娥五号”落月后，轨道飞行器将作为中继卫星在绕月轨道上做圆周运动，如图所示．设卫星距离月球表面高为h，绕行周期为T，已知月球绕地球公转的周期为T₀，地球半径为R，地球表面的重力加速度为g，月球半径为r，万有引力常量为G．试分别求出：

（1）地球的质量和月球的质量；
（2）中继卫星向地球发送的信号到达地球，最少需要多长时间？（已知光速为c，且h≤r≤R）