如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．
(1)求卫星B的运行周期．
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们还能相距最近？
地球赤道上的物体随地球自转的向心加速度为
，第一宇宙速度为
，地球半径为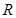
，同步卫星离地心距离为
，运行速率为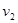
，向心加速度为
，则
A． |
B． |
C． |
D． |
已知地球同步卫星的轨道半径约为地球半径的6.6倍．一飞行器绕地球做匀速圆周运动的周期为3小时。若地球半径为R，则该飞行器绕地心飞行的轨道半径最接近
| A．0.83R | B．1.7R | C．1.9R | D．3.3R |
质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体，半径为R。
（1）已知地球质量为M，自转周期为T，引力常量为G。求此时卫星对地表的压力N的大小；
（2）卫星发射后先在近地轨道上运行（轨道离地面的高度可以忽略不计），运行的速度大小为v1，之后经过变轨成为地球的同步卫星，此时离地面高度为H，运行的速度大小为v2。
a．求比值
；
b．若卫星发射前随地球一起自转的速度大小为v0，通过分析比较v0、 v1、v2三者的大小关系。
某人造地球卫星在近似圆轨道上运行的过程中，由于轨道所在处的空间存在极其稀薄的空气，则
| A．如不加干预，卫星所受的万有引力将越来越小 |
| B．如不加干预，卫星运行一段时间后动能会增加 |
| C．卫星在近似圆轨道上正常运行时，由于失重现象卫星内的物体不受地球引力作用 |
| D．卫星在近似圆轨道上正常运行时，其速度介于第一宇宙速度和第二宇宙速度之间 |
质量为100 kg行星探测器从某行星表面竖直发射升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭，探测器从发射到落回出发点全过程的速度图象如图所示。已知该行星半径是地球半径的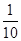
，地球表面重力加速度为10m/s2，该行星表面没有大气，不考虑探测器总质量的变化。求：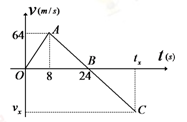
（1）探测器发动机推力大小；
（2）该行星的第一宇宙速度大小。
如图，若两颗人造卫星a和b均绕地球做匀速圆周运动，A.b到地心O的距离分别为r1、r2,线速度大小分别为v1 、v2。则 （ ）
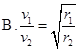
D.
火星的直径为地球的一半，质量为地球的十分之一，它绕太阳公转的轨道半径约为地球绕太阳公转的轨道半径的1.5倍，地球表面重力加速度约为10m/s2，从以上信息可知
| A．火星公转的周期比地球公转的周期短 |
| B．火星表面重力加速度约为4m/s2 |
| C．火星公转的向心加速度比地球公转的向心加速度大 |
| D．火星公转的线速度大于地球公转的线速度 |
以下说法正确的是
| A．丹麦天文学家第谷通过长期的天文观测，指出所有行星绕太阳运动的轨道都是椭圆，揭示了行星运动的有关规律 |
| B．电荷量e的数值最早是由美国物理学家密立根测得的 |
| C．库仑测出了引力常量G的数值 |
| D．万有引力定律和牛顿运动定律一样都是自然界普遍适用的基本规律 |
有a、b、c、d四颗地球卫星，a还未发射，在地球赤道上随地球表面一起转动，b处于地面附近近地轨道上正常运动，c是地球同步卫星，d是高空探测卫星，设地球自转周期为24h，所有卫星均视为匀速圆周运动，各卫星排列位置如图所示，则有
| A．a的向心加速度等于重力加速度g |
B．c在4 h内转过的圆心角是 |
| C．b在相同时间内转过的弧长最长 |
| D．d的运动周期有可能是23h |
某星球的质量约为地球质量的8倍，半径约为地球半径的2倍。已知地球的第一宇宙速度为7.9 km/s，则航天器在该星球表面附近绕星球做匀速圆周运动的速度大小约为多少？
已知引力常量G和下列某组数据，不能计算出地球质量．这组数据是（ ）
| A．地球绕太阳运行的周期及地球与太阳之间的距离 |
| B．月球绕地球运行的周期及月球与地球之间的距离 |
| C．人造地球卫星在地面附近绕行的速度及运行周期 |
| D．若不考虑地球自转，已知地球的半径及重力加速度 |
科学探测表明，月球上存在丰富的氧、硅、铝、铁等资源．设想人类开发月球，不断把月球上的矿藏搬运到地球上，假定经过长期的开采后月球与地球仍可看作均匀球体，月球仍沿开采前的轨道运行，则与开采前相比地球与月球间的万有引力将 ．（填“不变”“变大”或“变小”）
如图，足够大的光滑绝缘水平面上有三个带电质点，A和C围绕B做匀速圆周运动，B恰能保持静止，其中A、C两点与B的距离分别是L1和L2，不计三质点间的万有引力，则A和C的比荷（电量与质量之比）之比应是（ ）
A.
B.
C.
D.
粤公网安备 44130202000953号