高中物理万有引力定律及其应用试题

下列关于力的说法不正确的是
A.作用力和反作用力分别作用在两个不同的物体上 
B.太阳系中的行星均受到太阳的引力作用 
C 运行的人造地球卫星所受引力的方向不变
D.伽利略的理想实验说明了力不是维持物体运动的原因 

一艘宇宙飞船飞近某一新发现的行星，并进入靠近该行星表面的圆形轨道绕行数圈后，着陆在该行星上。飞船上备有以下实验器材：①精确秒表一只；②已知质量为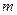的物体一个；③弹簧测力计一个。若宇航员在绕行时测出了飞船绕行星运行的周期为T，着陆后质量为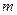的物体所受重力为F。并已知万有引力常量为G，行星的自转可忽略不计，试求出该星球的半径R及星球的质量M。

地球绕太阳的运动可视为匀速圆周运动，太阳对地球的万有引力提供地球运动所需的向心力，由于太阳内部的核反应而使太阳发光，在这个过程中，太阳的质量在不断减小（假如地球继续做圆周运动），根据这一事实可以推知，在若干年以后，地球绕太阳的运动情况与现在相比

A．向心加速度变小	B．运动频率变小
C．所受太阳的万有引力变大	D．运动角速度变大

宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其他星体对它们的引力作用。现已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆轨道上运行。设每个星体的质量均为m。万有引力常量为G。
（1）试求第一种形式下，星体运动的线速度和周期；
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？

为了探测星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为的圆轨道上运动，周期为。总质量为。随后登陆舱脱离飞船，变轨到离星球更近的半径为的圆轨道上运动，此时登陆舱的质量为则（）

A．	星球的质量为
B．	星球表面的重力加速度为
C．	登陆舱在 与 轨道上运动时的速度大小之比为
D．	登陆舱在半径为 轨道上做圆周运动的周期为

设“嫦娥1号”探月卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的1/81,月球的半径约为地球半径的1/4,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的速率约为 （     ）

A．0.4 km/s

B．1.8 km/s

C．11 km/s

D．36 km/s

如图所示，在同一轨道平面上，有绕地球做匀速圆周运动的卫星A、B、C，某时刻他们的连线与地球球心在同一条直线上，则 （     ）

A．经过一段时间，A回到原位置时，B、C也将同时回到原位置
B．卫星C的线速度最大
C．卫星B的周期比卫星A的周期大
D．卫星A的向心加速度最小

已知地球的半径为R，地球表面的重力加速度大小为g，万有引力常量为G，不考虑地球自转的影响．试求：
（1）卫星环绕地球运行的第一宇宙速度的大小；
（2）若卫星绕地球做匀速圆周运动且运行周期为T，求卫星运行的轨道半径r；
（3）由题干所给条件，推导出地球平均密度的表达式．

为了对火星及其周围的空间环境进行探测，我国预计于2011年10月发射第一颗火星探测器“萤火一号”．假设探测器在离火星表面高度分别为h1和h2的圆轨道上运动时，周期分别为T1和T2．火星可视为质量分布均匀的球体，且忽略火星的自转影响，万有引力常量为G．利用以上数据，可以计算出

A．火星的质量

B．“萤火一号”探测器的质量

C．火星对“萤火一号”探测器的引力大小

D．火星表面的重力加速度大小

天文工作者观测到某行星的半径为
r₀，自转周期为T₀，它有一颗卫星，轨道半径为r，绕行星公转周期为T。求：
（1）该行星表面的重力加速度g为多大？
（2）要在此行星的赤道上发射一颗同步人造卫星，使其轨道在赤道上方，则该同步卫星离地表的高度h为多大？

地球同步卫星的向心加速度为a₁，地面附近卫星的向心加速度为a₂，地球赤道上物体随地球自转的向心加速度为a₃，则有  

A．a1> a2> a3

B．a3> a2> a1

C．a2> a3> a1

D．a2> a1> a3

下图是某位同学设想的人造地球卫星轨道（卫星发动机关闭），其中不可能的是

北斗卫星导航定位系统，是我国自行研制开发的区域性有源三维卫星定位与通信系统，目前“北斗一号”已经成功运行，正在建设的“北斗二号”卫星导航系统空间段将由5颗高轨道静止卫星和30颗中低轨道非静止卫星组成．则下列“北斗二号”的卫星说法中正确的是

A．静止轨道卫星即同步卫星，它相对地球静止，所以它处于平衡状态

B．静止轨道卫星周期为一天，且轨道平面与赤道平面重合

C．高轨道卫星的线速度小于7.9km/s，中低轨道卫星的线速度大于7.9km/s

D．高轨道卫星的向心加速度小于中低轨道卫星的向心加速度

一宇航员抵达一半径为Ｒ的星球表面后，为了测定该星球的质量Ｍ，做如下实验，取一根细线穿过光滑的细直管，细线一端栓一质量为m的砝码，另一端连在一固定的测力计上，手握细直管抡动砝码，使它在竖直平面内做完整的圆周运动。停止抡动细直管，砝码可继续在同一竖直平面做完整的圆周运动。如图所示，观察测力计得到，当砝码运动到圆周的最低点时，测力计的读数为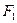；当砝码运动到圆周的最高点时，测力计的读数为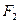。已知引力常量为Ｇ，试根据题中提供的条件和测量结果，求：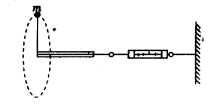

（1）该星球表面的重力加速度；
（2）该星球的质量Ｍ；
（3）该星球的第一宇宙速度。

已知地球质量为M，万有引力常量为G，现有一质量为m的卫星绕地球做匀速圆周运动，其轨道半径为r，求：
⑴卫星的线速度大小.  
⑵卫星在轨道上做匀速圆周运动的周期