高中物理平抛运动计算题

如图所示，传送带以5m/s的速度斜向上匀速运动，图中θ＝30°。在传送带底端P处轻轻放一个质量为4 kg的物块，物块由P点运动到顶端Q点，之后物块沿水平方向抛出，最终落入地面上某接收容器内。已知传送带的长度l_PQ="6.4" m，地面上的接收容器高度不计，物块与传送带间的动摩擦因数为μ＝，取g="10" m/s²。试求：

（1）物块从P点运动到Q点所用的时间；
（2）接收容器距离Q点的水平距离。

如图所示，已知倾角为θ=45°、高为h的斜面固定在水平地面上．一小球从高为H（h＜H＜h）处自由下落，与斜面做无能量损失的碰撞后水平抛出．小球自由下落的落点距斜面左侧的水平距离x满足一定条件时，小球能直接落到水平地面上．

（1）求小球落到地面上的速度大小；
（2）求要使小球做平抛运动后能直接落到水平地面上，x应满足的条件；
（3）在满足（2）的条件下，求小球运动的最长时间．

如图所示，小球由静止开始沿光滑轨道滑下，并沿水平方向抛出，小球抛出后落在斜面上．已知斜面的倾角为θ，斜面上与小球抛出点在同一水平面上，斜面长度为L，斜面上M、N两点将斜面长度等分为3段．小球可以看作质点，空气阻力不计．为使小球能落在M点以上，释放小球的位置相对于抛出点的高度h应满足什么条件？

如图所示，半径R=0.9m的光滑的半圆轨道固定在竖直平面内，直径AC竖直，下端A与光滑的水平轨道相切．一个质量m=1kg的小球沿水平轨道从A端以V_A=3m/s的速度进入竖直圆轨道，后小球恰好能通过最高点C．不计空气阻力，g取10m/s²．求：

（1）小球刚进入圆周轨道A点时对轨道的压力为多少？
（2）小球从C点离开轨道后的落地点到A点的距离为多少？

如图所示，图中的装置可测量子弹的速度，其中薄壁圆筒半径为R，圆筒上的a、b两点是一条直径上的两个端点（图中OO′为圆筒轴线）。圆筒以速度v竖直向下匀速运动。若某时刻子弹沿图示平面正好水平射入a点，且恰能经b点穿出。

（1）若圆筒匀速下落时不转动，求子弹射入a点时速度的大小；
（2）若圆筒匀速下落的同时绕OO匀速转动，求圆筒转动的角速度条件。

如图所示，斜面倾角为45°，从斜面上方A点处由静止释放一个质量为m的弹性小球，在B点处和斜面碰撞，碰撞后速度大小不变，方向变为水平，经过一段时间在C点再次与斜面碰撞。已知AB两点的高度差为h，重力加速度为g，不考虑空气阻力。求：

（1）小球在AB段运动过程中重力做功的平均功率P；
(2)小球落到C点时速度的大小。

如图所示，质量是1kg的小球用长为0.5 m的细线悬挂在O点，O点距地面高度为1m，如果使小球绕00′轴在水平面内做圆周运动，若细线最大承受拉力为12.5 N，(g=10m／s²).求：

(1)当小球的角速度为多大时，细线将断裂；
(2)线断裂后小球落地点与悬点的水平距离.

如图所示，在水平地面MN上方有一个粗糙绝缘平台PQ，高度为h=0.4m平台上方PR右侧有水平向右的有界匀强电场，PR左侧有竖直向上的匀强电场，场强大小均为E=1.1×l0⁴ N/C有一质量m=1.0×10^-3kg、电荷量为q= —1.0×10^-6C的滑块，放在距离平台左端P点L="0." 5m处，滑块与平台间的动摩擦因数现给滑块水平向左的初速度=4m/s，取g=10m/s²，求：

（1）滑块经过P点时的速度；
（2）滑块落地点到N点的距离

如图所示，质量为m的小球从A点水平抛出，抛出点距离地面高度为H，不计与空气的摩擦阻力，重力加速度为g。在无风情况下小球的落地点B到抛出点的水平距离为L；当有恒定的水平风力F时，小球仍以原初速度抛出，落地点C到抛出点的水平距离为3L/4，求：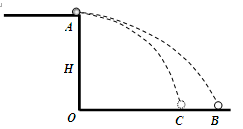

（1）小球初速度的大小； 
（2）水平风力F的大小；

如图所示，AB是固定在竖直平面内倾角=37⁰的粗糙斜面，轨道最低点B与水平粗糙轨道BC平滑连接，BC的长度为S_BC= 5.6m．一质量为M =1kg的物块Q静止放置在桌面的水平轨道的末端C点，另一质量为m=2kg的物块P从斜面上A点无初速释放，沿轨道下滑后进入水平轨道并与Q发生碰撞。已知物块P与斜面和水平轨道间的动摩擦因数均为μ=0.25，S_AB = 8m， P、Q均可视为质点，桌面高h = 5m，重力加速度g=10m/s²。

（1）画出物块P在斜面AB上运动的v-t图。
（2）计算碰撞后，物块P落地时距C点水平位移x的范围。
（3）计算物块P落地之前，全过程系统损失的机械能的最大值。

半径R = 40cm竖直放置的光滑圆轨道与水平直轨道相连接（如图所示）。质量m = 50g的小球A以一定的初速度由直轨道向左运动，并沿圆轨道的内壁冲上去。如果A经过N点时的速度v₁= 6m/s，A经过轨道最高点M后作平抛运动，平抛的水平距离为1.6m。求：

（1）小球经过M时速度多大；
（2）小球经过M时对轨道的压力多大；
（3）小球从N点滑到轨道最高点M的过程中克服摩擦力做的功是多少。（g=10m/s²）

某战士在倾角θ = 30°的山坡上进行投掷手榴弹训练。他从A点以某一初速度υ₀沿水平方向投出手榴弹，正好落在B点，测得AB 间的距离L= 90m。设空气阻力不计，取重力加速度g = 10m/s²。

（1）该型号手榴弹从拉动弦到爆炸需要T=5s的时间，若要求手榴弹正好落地爆炸，求战士从拉动弦到投出所用时间；
（2）求手榴弹抛出的初速度大小。

运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目。如下图所示，运动员驾驶摩托车的在AB段加速，到B点时速度为v₀=20m/s，之后以恒定功率P=1.8kW冲上曲面BCDE，经t=7.8s的时间到达E点时，关闭发动机后水平飞出。已知人和车的总质量m="180" kg，坡顶高度h=5m，落地点与E点的水平距离x=16m，重力加速度g=10m/s²。求摩托车在冲上坡顶的过程中克服阻力做的功。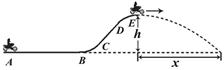

如图所示，一个人用一根长为R=1米，能承受最大拉力为F=74N的绳子，系着一个质量为m=1Kg的小球，在竖直平面内作圆周运动，已知圆心O离地面高h=6米。运动中小球在圆周的最低点时绳子刚好被拉断，绳子的质量和空气阻力均忽略不计，g="10" m/s²．求：

（1）绳子被拉断的瞬间，小球的速度v的大小？
（2）绳断后，小球落地点与圆周的最低点间的水平距离x多大？

如图，一个质量为0．6kg 的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧时无机械能损失）。已知圆弧的半径R=0．3m ，θ="60" ⁰，小球到达A点时的速度 v="4" m/s 。（取g ="10" m/s²）求：

（1）小球做平抛运动的初速度v₀；
（2）P点与A点的水平距离和竖直高度；
（3）小球到达圆弧最高点C时对轨道的压力。