高中物理平抛运动计算题

如图,在y>0的区域存在方向沿y轴负方向的匀强电场,场强大小为E，在y<0的区域存在方向垂直于xOy平面向外的匀强磁场。一个氕核 ¹ ₁H和一个氚核 ² ₁H先后从y轴上y=h点以相同的动能射出,速度方向沿x轴正方向。已知 ₁ ¹H进入磁场时,速度方向与x轴正方向的夹角为60°,并从坐标原点O处第一次射出磁场。 ₁ ¹H的质量为m,电荷量为q不计重力。求

（1） ₁ ¹H第一次进入磁场的位置到原点O的距离    

（2）磁场的磁感应强度大小    

（3） ₂ ¹H第一次离开磁场的位置到原点O的距离

如图所示，长为L、内壁光滑的直管与水平地面成30°角固定放置．将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M=km的小物块相连，小物块悬挂于管口．现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变．（重力加速度为g）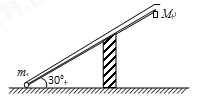

（1）求小物块下落过程中的加速度大小；
（2）求小球从管口抛出时的速度大小；
（3）试证明小球平抛运动的水平位移总小于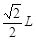

某战士在倾角为30^o山坡上进行投掷手榴弹训练。他从A点以某一初速度v₀沿水平方向投出手榴弹，正好落在B点，测得AB=90m。若空气阻力不计，（g=10m/s²）求：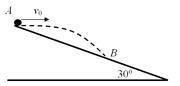

（1）手榴弹抛出的速度？
（2）从抛出开始经多长时间手榴弹与山坡间的距离最大？并求出此时手榴弹与山坡间的距离？

如图所示，在距地面高为H=45m处，某时刻将一小球A以初速度v₀=40m/s水平抛出，与此同时，在A的正下方有一物块B也以相同的初速度沿水平地面同方向滑出，B与水平地面间的动摩擦因数为μ=0.4，A、B均可视为质点，空气阻力不计，求：

（1）A球落地时的速度大小；
（2）A球落地时，A、B之间的距离。

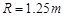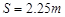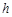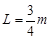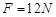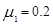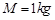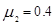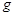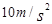如图所示，四分之一圆轨道OA与传送带相切相连，下方的CD水平轨道与他们在同一竖直面内。圆轨道OA的半径，传送带长，圆轨道OA光滑，AB与CD间的高度差为。一滑块从O点静止释放，当滑块经过B点时（无论传送带是否运动），静止在CD上的长为的木板（此时木板的末端在B点的正下方）在的水平恒力作用下启动，此时滑块落入木板中，已知滑块与传送带的摩擦因数，木板的质量，木板与CD间的摩擦因数为，取，求：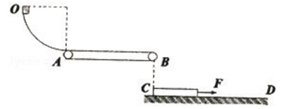

（1）如果传送带静止，求滑块到达B点的速度。
（2）如果传送带静止，求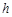的取值范围。
（3）如果传送带可以以任意速度传动，取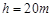，试判断滑块还能否落在木板上。

某滑板爱好者在离地h＝1.8m高的平台上滑行，水平离开A点后落在水平地面的B点，其水平位移X₁＝4.8m，(空气阻力忽略不计，g=10m/s²)，求：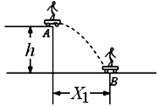

(1)人与滑板在空中运动的时间；
(2)人与滑板刚落地时速度的大小．

如图所示，质量为M＝1kg，长为L＝2.7m的木板，其上表面光滑且距离水平地面的高度为h＝0.2m，在水平面上向右做直线运动，A、B是其左右两个端点．当木板的速度v₀＝4m/s时对木板施加一个大小为3N的水平向左的恒力F，并同时将一个质量为m＝1kg的小球轻放在木板上的P点（小球可视为质点，放在P点时相对于地面的速度为零)，PB＝，经过一段时间，小球从木板脱离后落到地面上．已知木板与地面间的动摩擦因数μ=0.1，g取10m/s².求：
（1)小球从放到木板上开始至落到地面所用的时间；
（2)小球落地瞬间木板的速度．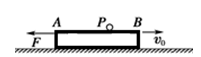

如图所示，一小球从平台上水平抛出，恰好落在临近平台的一倾角α=53°的光滑斜面顶端并下滑，已知斜面顶端与平台的高度差h=0.8m，重力加速度（sin53°=0.8，cos53°=0.6）求：

（1）小球水平抛出的初速度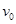是多少？
（2）斜面顶端与平台边缘的水平距离s是多少；
（3）若斜面顶端高H=20.8m，则小球离开平台后经多次时间到达斜面底端。

某人站在一平台上，用长L=0.6m的轻细线拴一个质量为m=0.6kg的小球，让它在竖直平面内以O点为圆心做圆周运动，当小球转到最高点A时，人突然撒手。经t=0.8s小球落地，落地点B与A点的水平距离x=4.8m，不计空气阻力，g=10m/s²。求：

（1）A点距地面高度h；
（2）人撒手前小球运动到A点时，绳对球的拉力F_T的大小。

如图所示，两光滑金属导轨，间距d=0.2m，在桌面上的部分是水平的，处在磁感应强度B=0.1T、方向竖直向下的有界磁场中．电阻R=3Ω．桌面高H=0.8m，金属杆ab质量m=0.2kg，电阻r=1Ω，在导轨上距桌面h=0.2m的高处由静止释放，落地点距桌面左边缘的水平距离s=0.4m，g=10m/s²．求：

（1）金属杆刚进入磁场时，R上的电流大小．
（2）整个过程中R上放出的热量．

如图，在粗糙水平台阶上静止放置一质量m=0.5kg的小物块，它与水平台阶表面的动摩擦因数μ=0.5，且与台阶边缘O点的距离s=5m．在台阶右侧固定了一个圆弧挡板，圆弧半径R=1m，圆弧的圆心也在O点．今以O点为原点建立平面直角坐标系．现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板．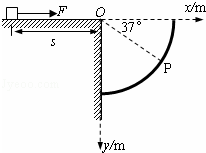

（1）若小物块恰能击中挡板上的P点（OP与水平方向夹角为37°），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的最短时间；
（3）改变拉力F的作用时间，使小物块击中挡板的不同位置，求击中挡板时小物块动能的最小值．

如图所示，水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m．在轨道所在空间存在水平向右的匀强电场，电场线与轨道所在的平面平行，电场强度E=1.0×10⁴N/C．现有一电荷量q=+1.0×10^﹣4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能通过半圆形轨道的最高点C，然后落至水平轨道上的D点．取g=10m/s²．试求：

（1）带电体在圆形轨道C点的速度大小．
（2）D点到B点的距离x_DB．
（3）带电体运动到圆形轨道B点时对圆形轨道的压力大小．
（4）带电体在从P开始运动到落至D点的过程中的最大动能．

如图所示，四分之三周长的细圆管的半径R=0.4m，管口B和圆心O在同一水平面上，D是圆管的最高点，其中半圆周BE段存在摩擦，BC和CE段动摩擦因数相同，ED段光滑；质量m=0.5kg、直径稍小于圆管内径的小球从距B正上方高H=2.5m的A处自由下落，从B处进入圆管继续运动直到圆管的最高点D飞出，恰能再次飞到B处．重力加速度g=10m/s²．求：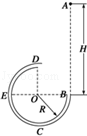

（1）小球飞离D点时的速度；
（2）小球在D点时对轨道的压力大小和方向；
（3）小球从B点到D点过程中克服摩擦所做的功．

在如图所示的平面直角坐标系内，x轴水平、y轴竖直向下。计时开始时，位于原点处的沙漏由静止出发，以加速度a沿x轴匀加速度运动，此过程中沙从沙漏中漏出，每隔相等的时间漏出相同质量的沙。已知重力加速度为g，不计空气阻力以及沙相对沙漏的初速度。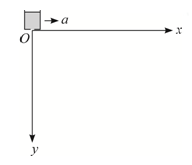

（1）求t₀时刻漏出的沙在t（t> t₀）时刻的位置坐标；
（2）t时刻空中的沙排成一条曲线，求该曲线方程。

如图所示，一小球（可视为质点）自平台上水平抛出，恰好落在临近平台的一倾角为α＝37°的斜面顶端，并刚好沿斜面下滑，已知斜面顶端与平台的高度差h＝0.45 m，求：
（重力加速度g取10 m/s²，sin37°＝0.6，cos 37°＝0.8）

（1）小球水平抛出的初速度v₀是多少？
（2）斜面顶端与平台边缘的水平距离s是多少？