高中物理平抛运动计算题

如图所示，质量为m的物体（可视为质点）沿光滑水平面向左以初速度v₀做匀速直线运动，到达B点时沿固定在竖直平面内、半径为R=40cm的光滑半圆轨道运动，并恰能到达最高点C点后水平飞出，最后落到水平面上的A点。不计空气阻力，g=10m/s²。求：

（1）物体的初速度v₀；
（2）A、B两点间的距离x。

如图所示，在距地面高为H＝45 m处，有一小球A以初速度v₀＝10 m/s水平抛出，与此同时，在A的正下方有一物块B也以相同的初速度v₀同方向滑出，B与地面间的动摩擦因数为μ＝0.5，A.B均可看做质点，空气阻力不计，重力加速度g取10 m/s²，求：

（1）A球从抛出到落地的时间和这段时间内的水平位移；
（2）A球落地时，A.B之间的距离。

如图，位于竖直水平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成，圆弧半径Oa水平，b点为抛物线顶点。已知h=2m，，s=，取重力加速度大小。

（1）一小环套在轨道上从a点由静止滑下，当其在bc段轨道运动时，与轨道之间无相互作用力，求圆弧轨道的半径；
（2）若环从b点由静止因微小扰动而开始滑下，求环到达c点时速度的水平分量的大小。

如图所示，一名滑雪运动员经过一段加速滑行后从O点水平飞出，经过3.0s落到斜坡上的A点。已知O点是斜坡的起点，斜坡与水平面的夹角θ=37⁰，运动员的质量m=60kg。不计空气阻力。（取sin37⁰=0.6,cos37⁰=0.8,g取10m/s²）求：

⑴O点与A点的距离L；
⑵运动离开O点时的速度大小；
⑶运动员落到A点时的动能。

如图所示，半径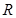=0.4m的光滑半圆环轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A．一质量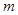=0.1kg的小球，以初速度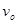=8m/s在水平地面上向左作加速度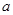=4m/s²的匀减速直线运动，运动4m后，冲上竖直半圆环，经过最高点B最后小球落在C点。取重力加速度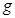=10m/s²。求：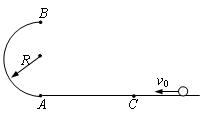

（1）小球到达A点时速度大小；
（2）小球经过B点时对轨道的压力大小；
（3）A、C两点间的距离。

(10分)如图所示，水平台AB距地面CD高h＝0.80m。有一小滑块从A点以6.00m/s的初速度在水平台上由于摩擦力作用做匀减速直线运动，并从平台边缘的B点水平飞出，最后落在地面上的D点。已知AB＝2.20m，CD= 2.00m。（不计空气阻力，g取10m/s²）。求：

（1）小滑块运动到B点时的速度大小；
（2）滑块与平台间的动摩擦因数。

、以初速度5米/秒水平抛出一个石子，落地点的竖直高度为5米，那么平抛运动的水平位移为多少？（g取10m/s²）

(6分)某同学对着竖直墙壁练习打乒乓球，假定球在墙面上以10m/s的速度沿水平方向反弹，落地点到墙面的距离为6m，重力加速度g=10m/s²，空气的阻力可忽略，求乒乓球在墙面上反弹点距水平地面的高度。

如图所示，是一次娱乐节目中的一个游戏示意图，游戏装置中有一个光滑圆弧形轨道，高为h，半径为R，固定在水平地面上，它的左端切线沿水平方向，左端与竖直墙面间的距离为x，直墙高为H，滑板运动员可从墙面的顶部沿水平方向飞到地面上。游戏规则是让一滑块从弧形轨道的最高点由静止滑下，当它滑到轨道底端时，滑板运动员立即以某一初速度水平飞出，当滑块在水平面上停止运动时，运动员恰好落地，并将滑块捡起就算获胜，已知滑块到达底端时对轨道的压力大小为F，重力加速度为g，求：（不计滑板的长度，运动员看作质点）

（1）滑块的质量；
（2）滑块与地面间的动摩擦因数：
（3）滑板运动员要想获胜，他飞出时的初速度多大？

如图所示，轨道ABCD的AB段为一半径R=0.2的光滑1/4圆形轨道，BC段为高为h=5的竖直轨道，CD段为水平轨道。一质量为0.1的小球由A点从静止开始下滑到B点时速度的大小为2/s，离开B点做平抛运动（g取10/s²），求：

①小球离开B点后，在CD轨道上的落地点到C的水平距离；
②小球到达B点时对圆形轨道的压力大小？
③如果在BCD轨道上放置一个倾角＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置。

宇航员站在一星球表面上的h高处,沿水平方向抛出一个小球,经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L;若抛出时的初速度增大两倍,则抛出点与落地点之间的距离变为L . 已知两落地点在同一水平面上.求该星球表面的重力加速度. 

如图所示，竖直平面内的半圆形轨道下端与水平面相切，B、C分别为半圆形轨道的最低点和最高点。小滑块（可视为质点）沿水平面向左滑动，经过A点时的速度,恰好通过最高点C.已知半圆形轨道光滑，半径R=0.40m，滑块与水平面间的动摩擦因数m =0.50，A、B两点间的距离L=1.30m。取重力加速度g=10m/s²。求：

（1）滑块运动到A点时速度的大小
（2）滑块从C点水平飞出后，落地点与B点间的距离x。

某星球质量为M，半径为R，可视为质量分布均匀的球体，一人在该星球表面上距星球表面高为h（h远小于R）处以初速度V₀水平抛出一个质量为m的小球，不计任何阻力，万有引力常量为G，求：
（1）抛球过程中人对小球所做的功W；
（2）星球表面的重力加速度g的大小。
（3）小球落到星球表面时的速度v的大小。

某星球的质量约为地球的9倍，半径约为地球的一半，若从地球上高h处平抛一物体，射程为60m，则在该星球上，从同样高度以同样的初速度平抛同一物体，求：（地球表面重力加速度g_地=10m/s²）
（1）该星球表面的重力加速度g是多少？（2）射程应为多少？

如图所示，小球由静止开始沿光滑轨道滑下，并沿水平方向抛出，小球抛出后落在斜面上。已知斜面的倾角为θ，斜面上端与小球抛出点在同一水平面上，下端与抛出点在同一竖直线上，斜面长度为L，斜面上M、N两点将斜面长度等分为3段。小球可以看作质点，空气阻力不计。为使小球能落在M点上，

（1）小球抛出的速度多大？
（2）释放小球的位置相对于抛出点的高度h是多少？（重力加速度为g）